Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Что означает понятие цикличность в применении его к процессу роста популяции? Цикличность – это ритм, в котором происходит ее эволюция; ритм, связанный с процессом роста и с четко обозначенными на шкале абсолютного времени фазами этого процесса, отмечающими его подъем, стабилизацию и стагнацию.

Если считать численность растущей популяции мерой ее эволюции, то ее экспоненциальный рост (независимо от его каузальной интерпретации) не может быть связан (причинно или функционально) с каким-либо циклическим эволюционным процессом. Дело в том, что рост популяции будет здесь однородным во времени и цикл ее эволюции, зависящий от растущей численности, может иметь любой период и любую фазу.

Что же касается гиперболического роста, то, во-первых, этот рост в силу своей нелинейности, выражаемой простейшим аналитическим законом, подразумевает системность растущей популяции, т. е. связность всех ее частей, поэтому общая численность популяции может служить здесь мерой, характеризующей ее эволюцию. И, во-вторых, рост этот по определению имеет одну особенность: точку на оси времени, в которой эта численность устремляется к бесконечности.

Циклы роста и развития могут быть введены здесь обратным отсчетом времени от точки сингулярности в прошлое с периодом, равным характерному времени. (Такое определение цикличности эволюции и развития в процессе гиперболического роста является, разумеется, чисто формальным. Подробнее см. главу «Законы роста численности изолированных популяций».)

Если связь между скоростью роста и численностью населения мира не является причинно-следственной, а является всего лишь сопутствующей, то должен существовать некий причинный закон (возможно, с постдетерминацией), который обеспечивает такой не автокаталитический рост. Кроме того, этот же причинный закон будет определять характерное время и характерную численность, которые являются по отношении к закону гиперболического роста населения мира в таком случае сторонними.

И, что особенно важно, так это то, что эти сторонние масштабы времени и численности должны быть характерными масштабами на всех этапах такого роста: в том числе на начальном его этапе, а также во время перехода. Поэтому, в случае роста населения Земли, значения этих констант, полученные для начала демографического перехода, могут быть использованы и при описании гиперболического роста.

Постоянную Форстера С = 187 млрд лет, имеющую размерность времени, можно представить в виде произведения постоянных роста тремя различными способами:

1.Исходя из нашей модели.

2.Исходя из модели Капицы.

3.Используя значение численности на момент завершения эпохи гиперболического роста и начала демографического перехода.

Все они дают для характерного времени τ и характерной численности М примерно одинаковые значения. Рассмотрим их по порядку, но сначала разберемся с обозначениями.

Почему главное число своей теории С.П. Капица обозначил заглавной буквой K? Однозначного ответа нет, но, скорее всего, по имени автора (Kapitsa), т. к. берет заглавную K по аналогии с обозначением безразмерного числа Рейнольдса Re, с которым Капица сравнивает свою постоянную. (Рейнольдсу было сложнее, т. к. R – это универсальная газовая постоянная и пришлось взять две буквы имени Re. Однако это привело к неоднозначности в понимании: то ли Re – это число Рейнольдса, то ли произведение универсальной газовой постоянной на заряд электрона.)

Теперь о константе К 5– почему такое странное обозначение? Дело в том, что в нашей модели рост населения мира сопоставляется росту биниальной иерархической сети четвертого ранга. Число носителей клаттера такой сети равно двойке, в показателе которой стоит также двойка в четвертой степени.

Это число примерно равно постоянной Капицы K, определяющей порядок численности населения Земли на момент начала гиперболического роста. А его квадрат, K 2= K 5= 4,3 млрд, равен числу носителей структурной единицы сети пятого ранга (т. е. ее клаттера). Характерная численность народонаселения М, соответственно, в k раз больше K 5: M = k*K 5= 4,72 млрд, где k = 1,1 – зомби-коэффициент.

Рис. 2. Постоянные роста биниальных иерархических сетей от первого ранга до восьмого и некоторые известные в математике и физике числа с ними связанные.

В нашей модели характерное время τ ≈ T/(2 13N 4) ≈ 40 лет(N 4= 42399 – полное число циклов сети человека, T = 13,8 млрд лет – время эволюции Вселенной). Характерная численность M = kK 5= 4,72 млрд(k =1,1 – зомби коэффициент, K 5= 65536 2– число узлов клаттера сети пятого ранга.) Постоянная Форстера C = M*τ = 4,72*40 = 188,8 млрд выводится нами теоретически.

С.П. Капица был первым, кто попытался выяснить смысл постоянной Форстера. Поскольку интервал времени в 187 млрд лет для растущей «популяции» Homo sapiens явно не имеет никакого смысла, он представил постоянную Форстера в виде произведения двух сомножителей С = τK 2. Где, согласно его подсчетам, время τ равно 41–42 годам и представляет собой некое характерное время человека.

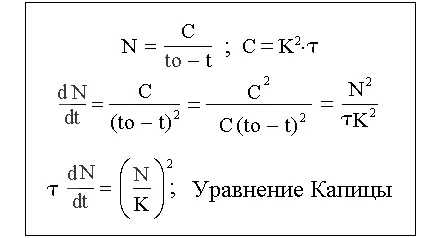
Рис. 3. Расщепление постоянной Форстера С на константы Капицы К и τ. Уравнение Капицы.

А K – безразмерная постоянная, равная 67000. Она определяет масштаб, в котором может быть измерена численность в начальную эпоху роста. Эта постоянная, которую С.П. Капица называет масштабным параметром, занимает центральное место в его теории:

«Это число занимает центральное место в теории роста, определяя все основные соотношения, возникающие при описании системной динамики человечества, являясь, в терминах синергетики, масштабным параметром. Следует отметить, что числами порядка K определяется эффективный размер группы, в которой проявляются коллективные признаки когерентного сообщества людей.

Таким может быть оптимальный масштаб города или района большого города, обладающего, как правило, системной самодостаточностью. В популяционной генетике величины такого порядка определяют численность устойчиво существующего вида или популяции, занимающей определенный ареал и экологическую нишу. Иными словами, это число является масштабом сообщества, имеющего генетическую или социальную природу» [1].

«Величина К определяет не только масштаб численности в начальную эпоху роста, но и дает оценку численности когерентной группы людей или племени – самодостаточной единице населения» [21]