Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Характерное время роста населения Земли τ, С.П. Капица уточнил следующим образом: он добавил член τ 2в знаменатель выражения для скорости изменения численности (1), а затем, проинтегрировав его, получил одну из ряда возможных гладких, с «выходом на полку» кривых, описывающих изменение численности до и во время перехода – рис. 4.

В результате сингулярность пропала, и можно было сравнивать фактические данные по населению мира за последние 250 лет и по формуле (2). Испробовав семь вариантов с τ = 20, 25, 33, 40, 42, 45, 55 лет, С.П. Капица пришел к выводу, что наилучшее приближение дает вариант № 5 с τ = 42 года.

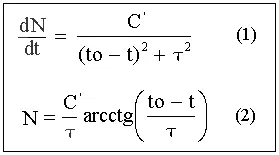
Рис. 4. Определение характерного времени τ путем замены гиперболы на время демографического перехода и времена близкие к нему – гладкой кривой с горизонтальной асимптотой.

Итак, согласно подсчетам С.П. Капицы, характерное время и характерная численность равны, соответственно: τ = 42 года, M = K 2= 67000 2= 4,49 млрд.

И, наконец, существует третий способ расщепления постоянной Форстера, который заключается в следующем:

На кривой роста численности населения Земли есть одна особенная точка: это тот момент времени и соответствующая ему численность, когда закон роста, остававшийся неизменным в течение многих тысяч лет, навсегда отходит от гиперболы. Эта дата, отделяющая эпоху гиперболического роста от эпохи перехода, согласно нашей теории, может быть использована для определения этих констант. Но определить их таким образом можно и без всякой связи с какой-либо теорией. Это мог сделать и С.П. Капица.

Действительно, рассмотрим теоретическую гиперболу с p = 1. Возьмем какую-то точку на оси времени и подсчитаем для нее численность населения мира и интервал времени, отделяющий ее от сингулярности гиперболы роста. Произведение этих величин равно постоянной Форстера, которая выступает здесь в качестве инварианта гиперболического роста. Продвигаясь по оси времени от прошлого к настоящему, дойдем до последней точки на кривой роста, для которой эта инвариантность будет еще выполняться (далее начинается демографический переход).

Эта точка является особенной, т. к. принадлежит как этапу роста, так и этапу перехода, поэтому ее координаты могут характеризовать как первый, так и второй. Если считать, что рост и переход представляют собой две последовательные стадии одного и того же процесса и могут быть описаны с помощью единых на всем их протяжении масштабов времени и численности, то определить эти масштабы можно следующим образом:

Примем за естественную меру для переменной «численность населения Земли» полное число живущих на тот момент времени, когда завершается эпоха гиперболического роста и начинается глобальный демографический переход. Иначе говоря, M – это численность населения мира в тот год, когда закон роста, остававшийся неизменным в течение многих тысяч лет, навсегда отходит от гиперболы.

В качестве масштаба времени выберем интервал времени, отсчитываемый от момента начала демографического перехода до точки сингулярности гиперболы демографического роста. Назовем этот интервал времени τ = C/M – характерным временем исторических изменений.

Момент времени, отмечающий завершение эпохи гиперболического роста, трудно определить по следующим причинам: во-первых, численность населения мира по годам во второй половине XX века известна лишь с точностью до нескольких процентов.

И, во-вторых, если исходить из нашей модели, гиперболический рост населения Земли хотя и представлял собой рост управляемый, подчиняющийся условию эквифинальности, тем не менее являлся по самой своей природе процессом случайным, что также не может не отразиться на точности выбора момента отхода роста от гиперболы.

Найти значения этих масштабов можно исходя из данного определения, однако высокой точности ожидать здесь не следует. Согласно мнению ряда исследователей, включая С.П. Капицу, переход начался где-то между 1965 годом и началом 1980-х прошлого столетия.

Начало демографического перехода С.П. Капица относит к моменту наивысшего набора скорости роста населения мира, а его конец – к моменту максимального спада прироста. Это не его определение, но оно полностью соответствует тому физикалистскому подходу к проблеме гиперболического роста населения планеты, которого он всегда придерживался.

При таком определении столь глобальные события, как конец эпохи гиперболического роста и момент завершения перехода (полное прекращение роста) определяются через мгновенную, «точечную» характеристику динамической системы растущее население Земли, такую как скорость роста численности.

Что вряд ли может считаться удовлетворительным, поскольку при таком физикалистском подходе остается необъясненной парадоксальная устойчивость гиперболического роста, возвращающая рост всегда на одну и ту же, по сути, предзаданную гиперболу. Скорее всего, здесь мы имеем дело с нестационарным случайным процессом N(t), направленным во все времена на одну и ту же гиперболу демографического роста.

Мгновенное значения скорости dN/dt в произвольный момент времени будет в таком случае всего лишь случайной величиной, и определять из динамики ее роста такие глобальные характеристики системы «растущее человечество», как начало и конец перехода – представляется неправильным.

Это неверное, по нашему мнению, определение и отодвинуло в прошлое дату начала перехода в расчетах С.П. Капицы примерно на 17 лет. Продолжительность демографического перехода в его модели составляет два характерных времени: 2τ = 42*2 = 84 года.

Если отложить от момента начала перехода по Капице характерное время τ, получаем ни о чем не говорящую, «безликую» дату 2007 год: 1965 + 42 = 2007. Дату, с которой не связано никакого глобального события истории, демографии и экономики и которая мало чем отличается от всех прочих дат первого десятилетия XXI века. (Мировой экономический кризис 2007–2012 гг. не был катастрофическим, и, кроме того, он никак не связан с демографическим переходом.)

Но если сместить начало перехода на 17 лет в будущее, то момент окончания первого цикла перехода (1982 + 40 = 2022) совпадет с сингулярностью гиперболы Форстера: исторической сингулярностью или сингулярностью Дьяконова – Капицы по нашему определению. Что еще раз указывает на ошибочность представления о том, что демографический переход начался в 1965 году.

Считая, что переход начался в конце семидесятых, начале восьмидесятых годов годов прошлого столетия и принимая для сингулярности гиперболы Форстера значение to = 2022–2032 г., получаем по самой грубой оценке для численности населения мира на момент начала перехода значение M ~ 5 млрд человеки для промежутка времени до сингулярности τ ~ 40–45 лет.