Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Все это говорит о том, что характерное время τ – это не усредненное время жизни человека, как полагал С.П. Капица, а длительность главного цикла экономики, истории и эволюции – Кондратьевского цикла. Время, за которое с системой «все человечество в целом» могут произойти качественные изменения. Его также можно назвать характерным временем исторических изменений.

Однако как бы то ни было, постоянные τ и К входят в уравнение Капицы и определяют в соответствии с этим уравнением два естественных масштаба: масштаб времени и масштаб численности. Единица исторического времени (его квант) равна постоянной τ, а естественная единица измерения численности населения Земли, в соответствии с уравнением Капицы, – это K.

Если численность измерять в единицах характерной численности Капицы n = N/K, а время – в числе циклов Кондратьева (не обязательно целом) до сингулярности: Т = (to – t)/τ, то закон гиперболического роста приобретает более простой вид: n = K/Т. (Если за масштаб для измерения численности взять M = K 2, то этот закон приобретает еще более простой вид: n = 1/Т.)

Являются ли постоянные Капицы фундаментальными постоянными эволюции человека? Определяют ли они эволюцию Homo sapiens, или это всего лишь эмпирические константы, входящие в закон гиперболического роста численности населения Земли?

Если говорить о физических постоянных, то, как известно, все они делятся на две основные группы: размерные и безразмерные. Значения безразмерных постоянных таких, как постоянная тонкой структуры, не зависят от систем единиц и должны определяться теоретически. Численные значения размерных постоянных зависят от выбора единиц измерения.

Размерные фундаментальные константы такие, как скорость света или постоянная Планка, могут выступать в виде естественных масштабов соответствующих физических величин. Это подчеркивал еще В. Гейзенберг:

«Универсальные постоянные определяют величины масштабов в природе, они дают нам характеристические величины, к которым можно свести все другие величины в природе». (Гейзенберг, 1959, с. 136.)

Вместе с тем в той же физике существует большое количество прикладных задач, в которых также есть соответствующие естественные масштабы важные именно для этих прикладных задач, но не столь фундаментальные, как постоянные с, h, G. В аэродинамике – это скорость звука, в гидродинамике – вязкость, которые определяют естественный масштаб измеряемой величины. Например, в аэродинамике «мах» – это мера скорости в единицах скорости звука.

С.П. Капица так и не пришел к окончательному выводу о смысле своих постоянных. На протяжении ряда лет он по разному определял и характерную численность, и характерное время. В последних своих работах характерное время τ он описывает как «эффективную продолжительность жизни человека» или как время близкое к среднему возрасту человека, а постоянную К сравнивает с безразмерным числом Рейнольдса в гидродинамике. [21]

В таком случае задача описания роста населения Земли в его модели – не более чем прикладная задача, а его постоянные – не более чем естественные масштабы для этой конкретной прикладной задачи. С этим трудно согласиться, потому что совершенно невозможно поверить в то, что рост населения Земли во все времена определялся, как полагал С.П. Капица, причинным законом квадратичного роста. Если бы это было так – не было бы никакой гиперболы роста и не было бы никаких постоянных роста.

Гиперболический рост населения Земли и связанные с ним константы роста, по нашему глубокому убеждению, был вызван неким неоткрытым и по настоящее время причинным законом с постдетерминацией, управлявшим ростом популяции Homo sapiens. Этот закон и определил постоянные роста, причем не только τ и К, но и to – момент сингулярности гиперболы Форстера. В таком случае постоянные Капицы – это постоянные эволюции человека и универсальной эволюции вообще.

Подобно тому как фундаментальные физические постоянные определяют естественные природные масштабы и, прежде всего, масштаб длительности и протяженности в физической картине мира, константы Капицы задают естественный масштаб измерения численности представителей человеческого социума, являющегося авангардной системой эволюции в текущую эпоху и масштаб времени, характеризующий темпы роста этой численности, – масштаб, в котором может быть измерено время эволюции человека.

Константы Капицы позволяют определить не только время начала антропогенеза, но и момент начала неолита, начала и завершения демографического перехода, а также оценить численность населения Земли во все времена. С помощью τ и К можно подсчитать продолжительность сокращающихся по закону прогрессии циклов эволюции и истории, а также полное число когда-либо живших на Земле людей. [1] Причем все это можно сделать как в рамках модели Капицы, так и на основе изоморфной ей сетевой модели.

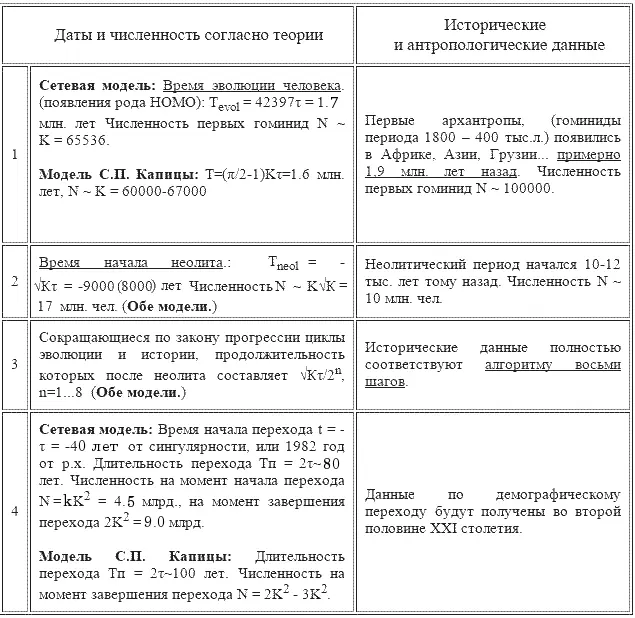
Таблица 1. Самые важные даты эволюции и истории человечества, рассчитанные теоретически с помощью постоянных Капицы τ и К. Приведены также современные научные данные по численности населения Земли в эти моменты времени.

Результаты расчетов в рамках первой и второй модели в первом приближении совпадают и полностью соответствуют данным демографии, истории и палеоантропологии – таблица 1. Все это говорит о том, что τ и К – фундаментальные постоянные эволюции человека.

Кроме того, об этом же говорит и полученная нами теоретическая зависимость численности от времени, полностью совпадающая с эмпирической гиперболой, описывающей рост населения Земли за последние сорок с лишним тысяч лет:

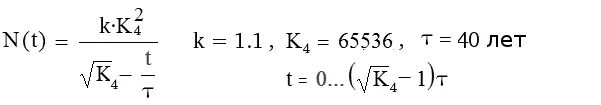
Рис. 1. Теоретическая гипербола, совпадающая с эмпирической гиперболой демографического роста. Отсчет времени ведется от момента начала неолита. Постоянная Капицы K ≈ K 4, весу клаттера сети четвертого ранга (точнее K = √k K 4).

Если бы константы τ и К не были постоянными эволюции человека – не было бы и никакой теоретической зависимости, описывающей гиперболический рост населения мира. Если же считать, что квант исторического времени, точнее его цикл (абсолютная разметка исторического времени на периоды постоянной длительности), существует, алгоритм восьми шагов отвечает действительности – такую формулу легко сконструировать.

Длительность исторического цикла τ равна здесь сорока годам, отсчет времени ведется от начала неолита. Гиперболический рост занимает 255 циклов; в 1982 году начинается демографический переход и формула на рис. 1 перестает правильно описывать рост. Сингулярность теоретической гиперболы, сингулярность Дьяконова – Капицы, наступает в момент времени t = 256τ.