Анатолий Молчанов - Население Земли как растущая иерархическая сеть

По неясным причинам С.П. Капица не связывает характерное время τ и характерную численность K с моментом начала перехода, что также является, по нашему мнению, большой ошибкой. (Скорее всего, по причине неверного определения начала перехода через мгновенную скорость роста численности dN/dt.) Кроме того, совершенно непонятно откуда вообще взялось значение С = 163 млрд лет, которое без всякого обоснования и каких-либо объяснений появляется в последней его работе [21]. Оно совершенно не согласуется с результатами работы Форстера и приведенными ниже оценками.

Определим константы Капицы, исходя из нашей гипотезы: характерная численность Капицы K = √kK 4= √1,1*2 16≈ 68700 (точность К зависит от точности в определении зомби-коэффициента k, доверительный интервал для которого нам неизвестен); характерное время находим по формуле τ = T 13/N 4. Где T 13– продолжительность 13-й эпохи универсальной эволюции или время эволюции человека; N 4– полное число циклов роста сети четвертого ранга, сети 65536; T 13= Тu/2 13, Тu = 13.81 ± 0.06 млрд лет – время эволюции Вселенной, N 4= 42399. Получаем τ = 39.75 ± 0.20 лет.

В заключение рассмотрим вопрос о точности, с которой известна постоянная Форстера.

1. Согласно расчетам Форстера и его коллег, значение постоянной С равно 179 ± 14 млрд лет. Но это ее значение справедливо лишь для эмпирической гиперболы с показателем p = 0.99. Если же положить p = 1, что соответствует теоретической гиперболе и, как мы это показали ранее, действительному закону роста, то значение постоянной Форстера должно быть несколько увеличено.

На пальцах это можно объяснить так: гипербола y = C/x 2при x > 1 ближе «прижимается» к оси 0X чем гипербола y = C/x и чтобы вернуть ее на позицию максимально близкую (на некотором интервале) к y = C/x нужно несколько увеличить С. В нашем случае гипербола с p = 0.99 отстоит на наименьшее расстояние от всех точек плоскости (N,t), отвечающих данным мировой демографии. Гиперболу с p = 1 нужно немного «приподнять» над осью 0t для того, чтобы максимально сблизить с оптимальной гиперболой с p = 0.99, т. е. немного увеличить С.

Авторы статьи «Судный день: Пятница, 13 ноября 2026 года» (Doomsday: Friday, 13 November, A.D. 2026) использовали в своих вычислениях 24 опорных значения времени и численности, полученные из большого числа источников разной степени надежности, однако никакие из них приведены не были. Поскольку воспользоваться этими данными и определить на их основе постоянную С при p = 1 невозможно, оценить ее можно только исходя непосредственно из результатов исследования. Для этого необходимо подобрать такую гиперболу с целочисленным p = 1, которая отстоит от эмпирической гиперболы Форстера на наименьшее «расстояние»:

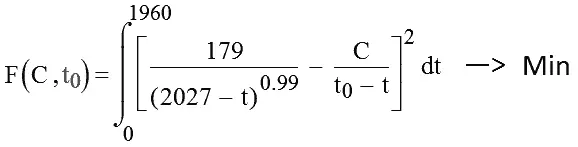
Рис. 1. Определение постоянной Форстера С для гиперболы с целочисленным показателем, исходя из условия минимальности «расстояния» между гиперболой с p = 1 и гиперболой Форстера с p = 0.99.

Значение С, которое является решением данной вариационной задачи, равно 188 млрд лет с точностью до одного-двух процентов, независимо от значения t 0в интервале [2022, 2028]. Поскольку у Форстера постоянная С определена с точностью 8 %, то эту же точность следует принять и для ее модифицированного значения. (Это и подобные ему определения постоянной С, основанные на усредненных значениях t 0и р, не могут, конечно, считаться математически строгими. Но позволяют, тем не менее оценить ее примерное значение, которое должно быть на несколько процентов больше, чем 179 млрд в формуле Форстера.)

2. Для непосредственного вычисления постоянной С при р = 1 воспользуемся данными по росту населения Земли, представленными в работе [40] Остина и Брюэра (A.L. Austin and J.W. Brewer). Хотя точек N(t i) у них, в отличие от работы Форстера и коллег, всего только 12 – все они взяты из трех авторитетных и признанных источников.

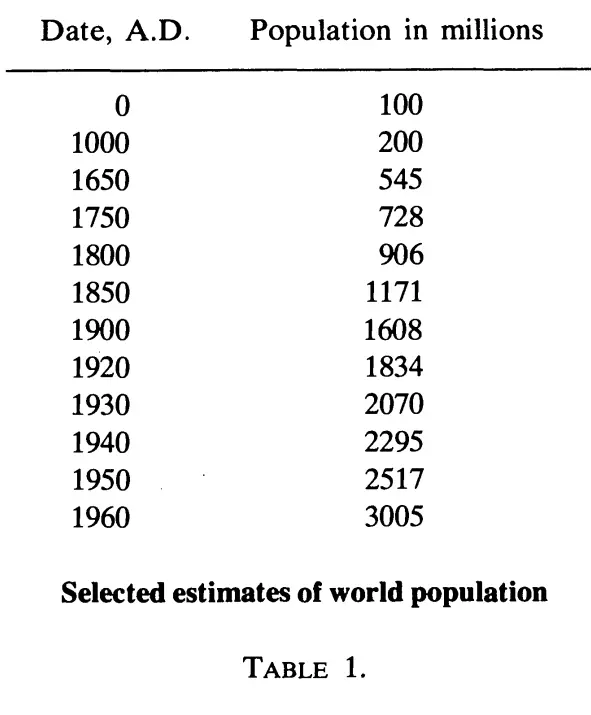
Таблица 1. Данные по населению мира от начала новой эры до 1960 года согласно A.L. Austin and J.W. Brewer [40].

Добавим еще одну точку N(1982) = 4.72 млрд, которая соответствует и теоретической гиперболе, и данным мировой демографии и обработаем все эти данные методом наименьших квадратов. В результате получим (в предположении p = 1, t 0= 2022) C = 194.3 млрд лет.

3. Мак-Эведи, Джоунс и Кремер выполнили собственный расчет, включив данные по неолиту и верхнему палеолиту. Значение постоянной Форстера С оказалось равным 189.6 млрд лет (p = 1, t 0= 2022) [13].

4. Примерно такое же значение для постоянной С находим и в работе [1] С.П. Капицы. Особенность его оценки, как мы уже отмечали ранее, заключается в том, что он определил постоянную Форстера, используя данные только за последние 250 лет (с учетом демографического перехода). В результате был получен следующий результат: C = K 2τ = 186 ± 1 млрд лет (τ = 42 ± 1, К = 67000, p = 1, t 0= 2027 ± 1).

5. И, наконец, определим значение постоянной Форстера на основе нашей модели, вычисляя ее по формуле: C = kK 4 2τ. Точность постоянной С сильно зависит от усредненного зомби-коэффициента k, значение которого подбирается исходя из критерия близости теоретической гиперболы данным мировой демографии. При k =1.1 C = 1.1*65536 2*(39.75 ± 0.2) = 187.8 ± ? млрд лет.

Итак, для постоянной Форстера имеем пять очень близких, независимых оценок. При этом точность ни одной из них нельзя считать установленной надежно:

1. Исходя из результатов работы Форстера и его коллег: С = 188 млрд лет.

2. Расчет на основе данных взятых у Остина и Брауэра: С = 194.3 млрд лет.

3. Работа Мак-Эведи, Джоунса и Кремера: С = 189.6 млрд лет.

4. Модель С.П. Капицы: С = 186 млрд лет.

5. Сетевая модель: С = 187.8 млрд лет.

Рассматривая эти результаты как ряд последовательных, независимых измерений величины С для ее среднего значения и среднеквадратического отклонения, получаем (при условии р = 1, t 0= 2022): С = 189.1 ± 1.3 млрд лет. Учитывая, что объем выборки очень мал, этот результат вряд ли можно считать корректным, и вопрос о точности, с которой известна постоянная С, остается открытым. Возможно ли вообще когда-либо решить этот вопрос, учитывая значительные пробелы и неточности в данных по численности населения Земли?

Современный научный подход к вопросам эволюции и развития опирается на представление о самоорганизации материи и самодостаточности элементарных законов с преддетерминацией, т. е. простейших физических законов, для объяснения всего спектра явлений материального мира, в том числе проблемы происхождения жизни, сознания, природы социальных явлений. Но так ли это?