Умберто Эко - Роль читателя. Исследования по семиотике текста [litres]

Отношения между мирами могут быть разными:

a) W i RW j , но не W j RW i : отношение бинарное, но не симметричное;

b) W i RW j и W j RW i : отношение бинарное и симметричное;

c) W i RW j , W j RW k , W i RW k : отношение бинарное и транзитивное;

d) предыдущее отношение – но к тому же и симметричное.

Если имеется два или большее число миров, то вышеобозначенные отношения могут изменяться в зависимости от следующих обстоятельств:

α) число индивидов и свойств одинаково во всех мирах;

β) число индивидов и свойств увеличивается по крайней мере в одном мире;

γ) число индивидов и свойств уменьшается по крайней мере в одном мире;

δ) свойства изменяются;

ε) (прочие возможные варианты, возникающие из комбинаций вышеназванных условий).

Что касается миров нарративных (воображаемых), то на данной основе можно было бы попытаться разработать типологию различных литературных жанров (см. интересные наметки Т. Павела – Pavel, 1975). Здесь мы рассмотрим лишь несколько примеров, интересных для нашей темы. Для начала возьмем пример с двумя мирами, имеющими одинаковое число индивидов и одинаковое число одинаковых свойств (не будем пока различать свойства существенные и случайные, «акцидентные»):

Рис. 8.11

Очевидно, что посредством некоторых комбинаторных манипуляций индивиды в мире W 1можно сделать структурно подобными индивидам в мире W 2 – и наоборот. Следовательно, отношение между мирами здесь бинарное и симметричное (W 1RW 2и W 2RW 1).

Рассмотрим теперь другой пример: в мире W 1имеется меньше свойств, чем в мире W 2. Представим себе (вслед за Хинтиккой – см. выше раздел 8.4.3), что в мире W 1есть свойства «круглый» и «красный», а в мире W 2индивид может иметь еще одно свойство: «крутящийся».

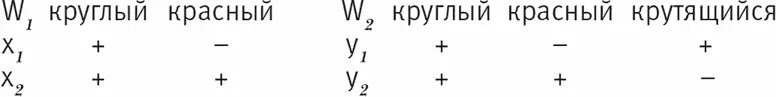
Рис. 8.12

Можно сказать, что в мире W 2 нетрудно породить индивиды из мира W 1 : достаточно в колонке «крутящийся» проставить минус (т. е. придать индивиду свойство «некрутящийся»):

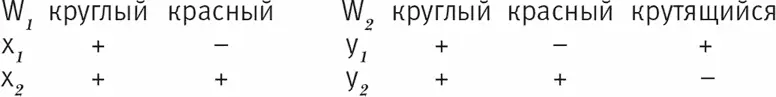
Рис. 8.13

Произведя такую операцию, мы видим, что y 4 структурно идентичен у 2 , в то время как y 3 – это совершенно новый индивид (который прежде в W 2 не существовал, но был потенциально представим).

Столь же очевидно, что невозможно проделать подобную операцию в мире W 1 , по отношению к миру W 2 : W 1 имеет более бедную матрицу (или мироструктуру), которая не может учесть наличие или отсутствие свойства «крутящийся». Стало быть, отношение между мирами W 1 и W 2 – несимметрично (W 2 R W 1 , но не W 1 RW 2 ). В рамках второго мира можно «вообразить», «представить себе» (т. е. воссоздать в силу гибкости его структуры) мир первый, но не наоборот. Подобная ситуация описана Э. Э. Эбботом [500]в его «Флатландии». Существо из трехмерного мира попадает в мир, где всего два измерения: гость может понять и описать мир, в котором он очутился, но обитатели этого мира не в состоянии даже представить себе своего гостя. Гость может проходить сквозь этот мир, обитатели которого мыслят лишь в терминах плоских фигур. Шар, имеющий три измерения, проходя через двухмерный мир, представляется в нем как ряд окружностей различного размера, но существа из этого мира не могут понять, почему пришелец постоянно меняет свой размер.

Рассмотрим еще один пример: к двум мирам из предыдущего примера прибавим третий мир W 3 , в котором есть различие между свойствами существенными и случайными («акцидентными»). В этом мире W 3 свойство «крутящийся» существенно для каждого индивида, так что никакой индивид не может одновременно и существовать, и быть некрутящимся (похоже, что так обстоит дело с планетами нашей солнечной системы):

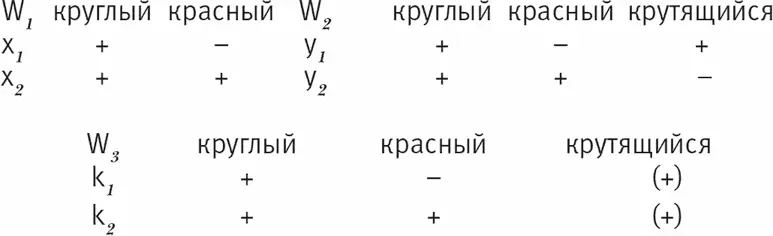
Рис. 8.14

Есть разные способы перейти от мира W 3к миру W 2. Если мы будем считать, что y 1обладает свойством «крутящийся» в качестве случайного («акцидентного»), то y 1(как и y 2) станет «сверхштатником» по отношению к прототипам в мире W 3. Если же мы решим сконструировать, исходя из мира W 3, такой у, у которого свойство «крутящийся» было бы существенным, то мы получим y 1как потенциальный вариант k 1. Поскольку от мира W 2легко перейти к миру W 1(как показано выше), то, следовательно, мы имеем между мирами W 1, W 2и W 3отношение бинарное и транзитивное (W 3RW 2, W 2RW 1, W 3RW 1), но не симметричное.

Чтобы перейти непосредственно от мира W 3к миру W 1, достаточно сконструировать такой мир, в котором каждый индивид будет иметь существенное свойство «некрутящийся». Тогда (в силу сказанного в разделе 8.6.3) индивиды из мира W 1, переопределенные таким образом, станут «сверхштатниками» по отношению к индивидам в мире W 3.

Поскольку в модальной логике тип отношений меняется в зависимости от используемой системы (Т, S4, S5 и т. д. – см., например: Hughes and Cresswell, 1968), то можно было бы поразмышлять о взаимоотношениях между вышерассмотренными примерами и различными модальными системами. Информированный читатель уже мог усмотреть некоторые аналогии между нашими матрицами миров и теми parlour games [501], которые приводятся в книге Хьюза и Крессуэлла (Hughes and Cresswell, 1968) в качестве примеров различных типов отношений. Но в рамках данного рассуждения нет никакой необходимости во что бы то ни стало отыскивать формальное подобие между нашими построениями и модальной логикой. Нас здесь интересует лишь то, как создавать структурные матрицы, пригодные для представления (репрезентации) текстовых миров, и как устанавливать правила трансформаций между ними.

Сведя свойства необходимые к свойствам существенным (определяемым как таковые в рамках топика), мы, разумеется, произвели удобное для нас упрощение проблемы. Но остается вопрос: что делать с так называемыми «логически необходимыми» истинами, к числу которых относятся, например, закон тождества и Modus Ponens?

Ответ таков: эти истины следует считать не свойствами индивидов какого-либо мира, а метаязыковыми условиями конструируемости матриц мира.