Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

К двум часам и одной минуте здоровье Ахиллеса оказывается, мягко говоря, подорвано: он лежит мертвый, а из его пятки торчит бесконечное количество отравленных стрел. Однако никого из богов нельзя обвинить в его смерти. У каждого из них есть превосходное оправдание, причем одно и то же: «Когда я выпустил свою стрелу в Ахиллеса, он уже был мертв, так как в его пятку попало бесконечное количество стрел. Я признаю, что стрелять в труп – дело неблаговидное, но это вовсе не значит, что меня можно обвинить в убийстве».

Вопрос: кто же убил Ахиллеса? И когда?

Вы, вероятно, уже заметили, что, как только мы начинаем задевать концепции вроде нуля и бесконечности, многие из «нормальных» законов перестают работать. Я расскажу вам об одном знаменитом мысленном эксперименте под названием «Космический корабль».

Попытайтесь представить себе, что произойдет с космическим кораблем, который летит по следующим правилам: первые полчаса он летит со скоростью 2 километра в час (то есть очень медленно по меркам космических кораблей). На следующую четверть часа его скорость несколько возрастает – до 4 километров в час. В течение следующей одной восьмой часа он летит со скоростью 8 километров в час – и так далее. Где этот космический корабль окажется через час?

Расчет несложен. За первые полчаса, пока корабль летит со скоростью 2 километра в час, он пролетит один километр. За следующие четверть часа, летя со скоростью 4 километра в час, он тоже пролетит один километр. И так далее и так далее: еще километр, и еще километр, и еще один. Легко видеть, что расстояние, которое преодолевает космический корабль, равно 1 + 1 + 1 +… Однако число единиц, которые нужно сложить, бесконечно, и, следовательно, бесконечна и итоговая сумма. Так где же наш космический корабль? По-видимому, нигде, потому что он должен оказаться на бесконечном расстоянии от точки запуска. Если бы космический корабль находился в какой-либо определенной точке, она была бы расположена на определенном расстоянии от точки запуска, но этого быть не может, так как корабль улетел на бесконечное расстояние. Где же он? Неизвестно. Поиски космического корабля продолжаются до сих пор.

Бесконечность нельзя найти ни в одной точке бесконечной прямой.

Докажите, не проводя никаких вычислений (то есть на словах), что:

.

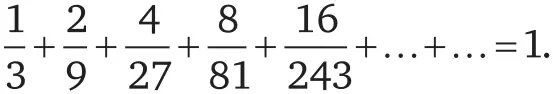
Одна из самых безумных, самых странных историй, какие я когда-либо читал, – это девятитомный роман родившегося в Ирландии английского писателя XVIII в. Лоренса Стерна «Жизнь и мнения Тристрама Шенди, джентльмена», опубликованный в 1759–1766 гг.

Как можно догадаться по названию, герой этой книги решил рассказать нам историю своей жизни и поделиться своими мыслями и мнениями. Но ее содержание не вполне соответствует ожиданиям читателя.

В книге девять томов, и одна из ее абсурдных идей состоит в том, что ни одно из событий в жизни главного героя не может быть рассказано просто: должны быть изложены все мельчайшие обстоятельства, связанные с таким событием даже самым отдаленным образом. Только в третьем томе (!) рассказчик добирается до момента своего рождения.

Тристрам сетует, что на рассказ об одном-единственном дне своей жизни ему требуется целый год. Бертран Рассел как-то отметил [36] В частности, в уже упомянутых работах «Математика и метафизики» и «Основания математики». , что если бы этот джентльмен прожил бесконечно много дней, он вполне смог бы рассказать всю историю своей жизни. В самом деле? С одной стороны, до каждого из дней его жизни в конце концов дошла бы очередь в повествовании. О 10 000-м дне своей жизни он рассказал бы на 10 000-м ее году. С другой стороны, каждый проходящий день увеличивает разрыв между жизнью прожитой и жизнью описанной еще на один год. Получается своего рода состязание Ахиллеса с черепахой, в котором Ахиллес пробегает целый год, а черепаха – всего лишь день. Но, поскольку в распоряжении черепахи имеется бесконечное время, она рано или поздно добирается до всех тех мест, в которых побывал Ахиллес.

С незапамятных времен бесконечное волновало человека более чем какой-либо другой вопрос. По-видимому, не существует другой идеи, которая вдохновляла бы, но и тревожила бы человеческий разум сильнее, чем концепция бесконечности; но именно по этой причине она и нуждается в разъяснении более чем какая бы то ни было другая концепция.

Эти слова взяты из статьи «О бесконечном» (Über das Unendliche) [37] Matematische Annalen 95 (1926). P. 161–190. Доклад, прочитанный в июне 1925 г. на съезде математиков, организованном Вестфальским математическим обществом в Мюнстере в память Вейерштрасса. великого математика XX в. Давида Гильберта (1862–1943).

Внимательно изучив первую часть той книги, которую вы держите в руках, вы можете заметить, что главная ее героиня – «бесконечность»: царство чисел есть царство бесконечное; и многие, а может быть, и большинство из ее загадок и секретов связаны, прямо или косвенно, с концепцией бесконечности.

Математика – наука бесконечности.

Предметом, который больше всего увлекал меня на первом курсе математического факультета университета, была теория множеств. Это название не кажется особенно привлекательным и даже приблизительно не описывало того, что изучалось в этом курсе. Начало не предвещало ничего хорошего: поразительно скучные определения, аксиомы и соотношения. Но уже через два занятия я понял, что этот курс на самом деле должен называться теорией бесконечных множеств, потому что речь в нем идет именно о бесконечном, с демонстративным пренебрежением к завету Галилео Галилея, призывавшего этим не заниматься. Кроме того, обсуждение бесконечности не было затемнено какими-либо метафизическими или теологическими соображениями – а я уже был знаком с такими взглядами, и некоторые из них – например антиномии Канта, концепции Николая Кузанского или мировоззрение Джордано Бруно (на которого Николай Кузанский оказал большое влияние) – меня весьма вдохновляли. Но теперь все было совсем по-другому, и я чувствовал, что передо мной разворачивается нечто не похожее ни на что из того, что я знал раньше. У меня было предчувствие, что мне откроется нечто чудесное.