Владимир Арнольд - Теория катастроф

Колчан на рис. 82 слева прост, справа непрост (см. пример 1).

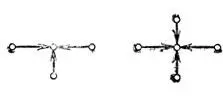
Рис. 82. Простой и непростой колчаны

Оказывается, все связные простые колчаны получаются произвольной расстановкой стрелок на изображенных на рис. 83 диаграммах Дынкина, образующих две бесконечные серии и три исключительные диаграммы .

Простые особенности каустик и волновых фронтов также образуют две бесконечные серии А kи D kи три исключительные особенности Е k(начальные члены серий изображены на рис. 34 — 45).

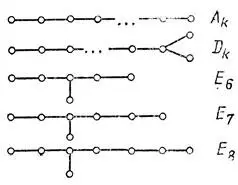
Рис. 83. Диаграммы Дынкина, определяющие простые колчаны

Группы симметрий правильных многогранников в трехмерном пространстве также образуют две бесконечные серии и три исключения (исключения — группы симметрий тетраэдра (Е 6), октаэдра (Е 7) и икосаэдра (Е 8), серии — группы правильного многоугольника и правильного диэдра, т. е. двустороннего многоугольника с окрашенными в разные или одинаковые цвета гранями).

На первый взгляд, функции, колчаны, каустики, фронты и правильные многогранники не связаны между собой. На самом деле соответственные объекты не случайно обозначены одинаково: например, из икосаэдра можно построить функцию х 2+ у 3+ z 5, а из нее — диаграмму Е 8, а также каустику и волновой фронт того же имени.

Легко проверяемым свойствам одного из соответствующих друг другу объектов соответствуют не обязательно очевидные свойства других. Таким образом, связи между всеми А, D, Е-классификациями используются для одновременного изучения всех простых объектов, несмотря на то, что происхождение многих из них (например, связей между функциями и колчанами) остается необъясненным проявлением загадочного единства всего сущего.

По словам поэта:

Описание в терминах теории особенностей было найдено в 1983 г. для всех групп Кокстера, порожденных отражениями в евклидовых пространствах, включая некристаллографические, вроде Н 3и Н 4.

Группы В k, С kи F 4связаны с краевыми особенностями функций (1978). Катастрофисты, кажется, все ещkkе не заметили связей теории краевых особенностей с простейшими (и важнейшими) случаями так называемой теории несовершенных бифуркаций . Более сложные случаи последней связаны с теорией Горюнова проектирований полных пересечений, которая является далеким обобщением теории краевых особенностей. В теории Горюнова, в частности, исключительная группа F 4оказывается родоначальником целого семейства особенностей F k, k ≥ 4.

Геометрическая интерпретация каустики F4 найдена И. Г. Щербак. Рассмотрим поверхность с краем в обычном трехмерном евклидовом пространстве. Каустика поверхности с краем состоит из трех поверхностей: фокального множества исходной поверхности (образованного ее центрами кривизны), фокального множества граничной кривой (являющегося огибающей семейства нормальных плоскостей) и поверхности, составленной из нормалей к исходной поверхности в граничных точках. Для поверхностей с краем общего положения в отдельных точках край касается направления главной кривизны. В окрестности фокальной точки на нормали к поверхности, проведенной в такой точке края, каустика поверхности локально диффеоморфна каустике группы F 4(рис. 84).

Н 3, группа симметрий икосаэдра, связана с перестройками эвольвент плоской кривой вблизи ее точки перегиба. В соответствующей плоской задаче об обходе препятствий график многозначной функции времени диффеоморфен многообразию нерегулярных орбит группы Н 3; он диффеоморфен также объединению касательных к кривой х = t, у = t 3, z = (О. В. Ляшко, О. П. Щербак). В задаче об обходе препятствия в трехмерном пространстве то же многообразие описывает особенность фронта в некоторых точках на поверхности препятствия.

Н 4— это группа симметрий правильного 600-гранника в четырехмерном евклидовом пространстве. Чтобы описать этот многогранник, начнем с группы вращений икосаэдра. При двулистном накрытии SU(2) → SO(3) эта группа из 60 вращений накрывается "бинарной группой икосаэдра" из 120 элементов. Группа SU(2) естественно изометрична трехмерной сфере, и 120 элементов бинарной группы образуют набор вершин искомого правильного многогранника в четырехмерном пространстве.

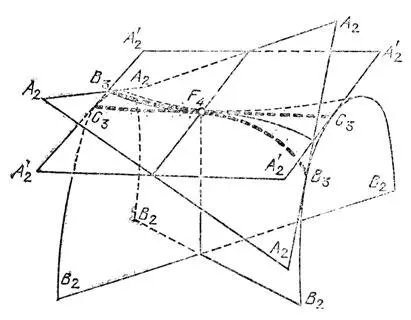
Рис. 84. Каустика группы F4 — типичная особенность фокального множества поверхности с краем

Рассмотрим теперь задачу об обходе препятствия в трехмерном пространстве. График (многозначной) функции времени является гиперповерхностью в четырехмерном пространстве-времени. Для задачи об обходе препятствия общего положения эта гиперповерхность локально диффеоморфна многообразию нерегулярных орбит группы Н 4в некоторой точке. А именно, нужная точка лежит на касательной к геодезической на поверхности препятствия, имеющей в параболической точке касания асимптотическое для поверхности направление (О. П. Щербак, 1984).

Не претендуя на полноту, я приведу здесь несколько ярких работ, авторы которых рассматривали особенности, бифуркации и катастрофы в системах общего положения, возникающих в различных областях знания.

Каустики встречаются уже у Леонардо да Винчи, название им дал Чирнгаузен.

В 1654 г. Гюйгенс построил теорию эволют и эвольвент плоских кривых, обнаружив одновременно устойчивость точек возврата на каустиках и волновых фронтах (т. е. сборок соответствующих отображений). Перестройки фронтов на плоскости исследовались Лопиталем (около 1700 г.) и Кэли в 1868 г.

Гамильтон в 1837 — 1838 г. применил исследование критических точек семейств функций к изучению особенностей систем лучей в геометрической оптике, вроде конической рефракции и двойного лучепреломления.