Владимир Арнольд - Теория катастроф

Тем самым мы решили задачу о топологическом строении неособой комплексной алгебраической кривой степени n (сфера с ручками, возникшая в этой конструкции, называется римановой поверхностью кривой) [9] Между прочим, из топологических свойств тора (а именно из того, что пара меридианов делит тор на две части) следует, что периоды колебаний с одинаковой полной энергией в обеих ямах механической системы с потенциальной энергией четвертой степени одинаковы (на торической римановой поверхности множества уровня энергии — фазовые кривые обеих ям — разные меридианы). .

Что же касается топологического строения вещественной кривой степени n, то оно до сих пор известно лишь для кривых малой степени (неизвестно уже, как могут располагаться ветви кривой степени 8 на плоскости).

Подобно теории кривых, теория особенностей также упрощается при переходе в комплексную область; многие явления, кажущиеся с вещественной точки зрения совершенно загадочными, в комплексной области получают прозрачное объяснение.

Рассмотрим, например, строение простейших критических точек комплексных функций (т. е. комплексификацию теории максимумов и минимумов).

Для вещественной функции критические точки связаны с перестройками линий или поверхностей уровня. Например, вещественная линия уровня х 2+ у 2= с функции f = х 2+ у 2пуста при с < 0и является окружностью при с > 0. Для функции х 2— у 2перестройка иная: асимптоты гиперболы х 2— у 2= c по-разному соединены ветвями этой гиперболы в зависимости от знака с. В этих примерах единственное критическое значение с = 0. Многообразия критического уровня — негладкие, некритического — гладкие.

В комплексном случае ось значений функции становится плоскостью комплексного переменного с. Критические значения лежат в этой плоскости изолированно и не делят ее на части. Поэтому многообразия уровня с при всех некритических значениям с устроены топологически одинаково. Если с, изменяясь, проходит через критическое значение, то никакой перестройки не происходит: многообразие уровня, правда, становится особым в момент прохождения с через критическое значений, но затем мгновенно возвращается в первоначальное состояние.

В комплексном случае вместо того, чтобы проходить через критическое значение, нужно обходить вокруг него (проявление общего принципа, согласно которому комплексным аналогом вещественного понятия "край" является "разветвленное накрытие").

Итак, рассмотрим на плоскости комплексного переменного с путь, обходящий критическое значение.

Каждой точке этого пути отвечает неособое многообразие уровня, f = с. При непрерывном изменении с многообразие уровня непрерывно меняется, оставаясь топологически таким же.

Иными словами, мы можем сопоставить каждой точке начального многообразия уровня близкую точку близкого многообразия уровня так, что получится взаимно-однозначное взаимно-непрерывное соответствие между обоими многообразиями уровня. Таким образом, мы получаем отождествление исходного многообразия уровня с многообразием близкого уровня с.

При непрерывном изменении с это отождествление непрерывно меняется, и в конце концов, когда с возвращается к исходному положению, мы получаем отождествление исходного многообразия уровня с самим собой. Это отождествление называется монодромией .

Итак, монодромия есть взаимно-однозначное и взаимно-непрерывное отображение многообразия неособого уровня на самого себя. Оказывается, это отображение — вовсе не тождественное преобразование: когда с делает полный оборот вокруг критического значения, возвращается на место лишь многообразие уровня с, а вовсе не его отдельные точки [10] Ситуация здесь в точности такая же, как с листом Мёбиуса. При непрерывном обходе вдоль осевой окружности листа Мёбиуса мы можем непрерывно отождествлять поперечные ей отрезки. Но когда мы впервые вернемся к исходному отрезку, полученное отождествление этого отрезка с самим собой будет менять местами его концы. .

Чтобы понять, что происходит при монодромии с точками многообразия неособого уровня, рассмотрим пример

f (х, у) = х 2+ у 2.

Изучим прежде всего многообразие неособого уровня х 2+ у 2= с, с ≠ 0. В вещественном случае это уравнение определяет окружность, нас же интересует "комплексная окружность" — множество точек (х, у) плоскости двух комплексных переменных, сумма квадратов (комплексных) Координат которых имеет фиксированное значение.

Мы уже знаем, что эта поверхность топологически устроена как цилиндр в четырехмерном пространстве.

Оказывается, монодромия поворачивает каждую из составляющих цилиндр окружностей на свой угол, меняющийся непрерывно от нуля на одном основании до 2π на другом. Таким образом, оба края цилиндра поточечно остаются на месте, в то время как поверхность перекручивается на целый оборот, так что, например, образующая цилиндра превращается в спираль, делающую на пути от одного основания к другому полный оборот вокруг цилиндра (рис. 76).

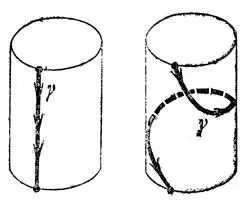
Рис. 76. Скручивание Дена — монодромия функции х 2+ у 2

Чтобы понять, почему это так, исследуем подробнее "комплексную окружность". Уравнение ее можно записать в виде у = √с — х 2. Из этой формулы видно, что каждому (комплексному) значению х соответствует пара значений у, за исключением х = ± √с, — каждому из этих двух особенных значений х соответствует единственное (нулевое) значение у.

Следовательно, график комплексной "двузначной функции" у = √с — х 2распростерт над плоскостью комплексной переменной х двулистно, причем оба листа соединены только в двух точках. Однако разделить оба листа, удалив лишь эти две точки, не удастся. В самом деле, заставим х обойти одну из этих точек по малому контуру, охватывающему ее один раз. Соответствующее значение у, непрерывно меняясь, вернется не к прежнему значению, а к другому. Действительно, из формулы

с — х 2= (√с — х) (√с + х)

видно, что при обходе х вокруг одной из точек ± √с, аргумент одного из сомножителей меняется на 2π, а другого не меняется. Значит, аргумент у меняется при указанном обходе на π, т. е. у меняет знак и переходит с одного листа на другой.

При двукратном обходе х вокруг точки √с величина у возвращается к исходному значению. Точки х = ± √с называются точками ветвления функции у = √с — х 2.

Чтобы лучше представить себе поверхность, заданную этой функцией, соединим обе точки ветвления отрезком. Если точка х гуляет по плоскости, не пересекая этого отрезка, то у возвращается к первоначальному значению всякий раз, когда х описывает замкнутый путь. Действительно, однократный обход любой из точек ветвления меняет лишь знак у, поэтому обход всего отрезка не меняет знака у.