Наум Виленкин - В поисках бесконечности

Математики той эпохи не подозревали, что существуют функции и линии, свойства которых совсем не похожи на свойства таких "добропорядочных" функций, как многочлены, тригонометрические, показательные функции и т. д. Но в разработанном ими математическом аппарате уже содержался динамит, который впоследствии и взорвал кажущееся благополучие. Этим динамитом оказалась теория бесконечных рядов. Первоначально такие ряды возникли, чтобы облегчить вычисление значений функций. Но потом они превратились в способ получения новых функций. И тут оказалось, что при сложении столь хороших функций, как многочлены, по мере добавления новых членов начинают выступать все более мелкие дрожания будущей бесконечной суммы, и в конце концов получается функция, совсем не похожая по своим свойствам нате, которыми занимался классический анализ. Поведение таких функций напоминало математикам-классикам сумасшедший дом. Так что и здесь понятие бесконечности, идея о возможности сложить бесконечно много слагаемых, оказало революционизирующее влияние на развитие науки.

А теперь позвольте пригласить вас на прогулку по математической кунсткамере, где собраны некоторые экспонаты, которые столь же отличаются от знакомых со школьных или вузовских времен математических образов, как ихтиозавры или какие-нибудь трицератопсы от современных животных.

Необычной является уже сама функция Дирихле, о которой говорилось выше. Ведь на самом маленьком отрезке оси абсцисс бесконечно много и рациональных чисел и иррациональных чисел. Но функция Дирихле для рациональных чисел равна единице, а для иррациональных — нулю. Поэтому когда x пробегает ось абсцисс, то значение функции все время прыгает от 0 к 1 и обратно. Построить график этой функции совершенно невозможно, потому что эта функция во всех точках разрывна.

Но и среди непрерывных функций есть функции с неожиданными свойствами. Например, может ли непрерывная функция иметь на конечном отрезке бесконечно много максимумов и минимумов? На первый взгляд это совершенно невозможно. Ведь функция должна успеть опуститься из точки максимума в точку минимума, потом опять подняться в точку максимума и т. д. Как же ей сделать все это на конечном отрезке? Тем не менее оказалось, что такие странные функции существуют, причем построить их совсем нетрудно.

Построим такую функцию на отрезке [0, 1]. Для этого разделим отрезок пополам и построим на левой половине равносторонний треугольник. Теперь разделим оставшуюся правую половину снова на две равные части и на части [ 1/ 2, 3/ 4] построим второй равносторонний треугольник. Выполним описанную операцию бесконечно много раз. У нас получится "горная цепь", состоящая из бесконечного числа вершин, постепенно опускающаяся к точке 1 (рис. 12). Примем полученную ломаную за график функции f(x). Тогда функция будет определена в каждой точке отрезка [0, 1], за исключением крайней правой точки 1. В этой точке положим f(1) = 0.

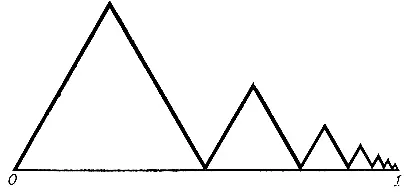
Рис. 12

Так как при приближении к точке 1 высоты вершин стремятся к нулю, полученная нами функция непрерывна во всех точках отрезка [0, 1]. А число максимумов и минимумов на этом отрезке бесконечно велико!

Математику XVIII в., чтобы построить такую странную функцию, понадобилось бы долго комбинировать различные функции, прежде чем он догадался бы, что функция

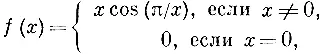
имеет бесконечно много максимумов и минимумов на отрезке [0, 1].

Но функции с бесконечным числом максимумов и минимумов были лишь началом неприятностей, ожидавших математиков. Джинн только начал выходить из бутылки.

У функции, которую мы построили в предыдущем пункте, есть лишь одна точка, около которой бесконечно много максимумов и минимумов, а именно точка 1. Сейчас мы построим другую функцию, у которой таких точек будет куда больше.

Предположим, что на отрезок [0, 1] оси абсцисс падает сверху дождь. Для защиты от дождя поступим следующим образом. Разделим отрезок [0, 1] на три равные части и возведем над средней частью палатку в форме равностороннего треугольника. Она защитит от дождя все точки средней части (кроме концов этой части, то есть точек 1/ 3и 2/ 3). Теперь каждую из оставшихся двух частей снова разделим на три равные части и защитим средние части палатками той же формы (но втрое меньшего размера).

У нас получится линия, изображенная на рис. 13. На третьем шаге процесса мы построим еще четыре палатки, потом еще восемь и т. д.

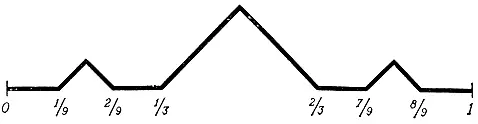
Рис. 13

Возникает вопрос: все ли точки отрезка защищены получившейся пилообразной линией или остались точки, которые дождь намочит? Некоторые из таких "мокрых" точек указать легко — ими являются концы защищаемых отрезков (то есть такие, как 1/ 3, 2/ 3, 1/ 9, 2/ 9, 7/ 9, 8/ 9и т. д.). Все эти точки остаются без защиты при возведении соответствующей палатки, а последующие палатки их тоже не защищают. Легко видеть, что таких концов будет бесконечное, но счетное множество.

Оказывается, что кроме этого счетного множества "мокрых" точек найдется еще целый континуум таких точек. Чтобы описать их, удобно прибегнуть к троичной системе счисления, в которой все числа записываются с помощью всего лишь трех цифр: 0, 1 и 2. В этой системе счисления число "семь" записывается в виде 21, а дробь 1/ 4— в виде 0,02020202... (чтобы убедиться в этом, надо вспомнить правило суммирования геометрической прогрессии).

Теперь мы уже можем точно сказать, какие точки останутся "мокрыми" после того, как все защитные палатки будут построены. Первая палатка защищает точки, лежащие между 1/ 3и 2/ 3. Но это те самые точки, которые в троичной системе имеют запись вида

0,1... ,

где точками обозначена любая комбинация цифр 0, 1 и 2 (точно так же, как в десятичной системе счисления между точками 1/ 10и 2/ 10лежат все точки, десятичная запись которых начинается с цифры 1, то есть имеет вид 0,1...). После первого шага "мокрыми" останутся точки, троичная запись которых имеет вид

0,0...

или вид

0,2...

Точно так же доказывается, что после возведения двух палаток на втором шаге мокрыми остаются лишь точки, троичная запись которых начинается с одной из следующих четырех комбинаций:

Итак, шаг за шагом защищаются от дождя точки, в троичную запись которых входят единицы. В конце концов останутся "мокрыми" лишь точки, которые можно записать в троичной системе счисления, не используя 1.