Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

Первым из них в 1735 г. стала загадка, связанная с городом Кёнигсберг в Пруссии (ныне Калининград в России). В этом городе, расположенном на реке Прегель, имеется два острова, связанных друг с другом и с берегами реки семью мостами. Загадка состояла в том, чтобы найти такой маршрут через город, который прошел бы по каждому мосту ровно один раз. Начало и конец маршрута могли находиться в разных местах. Эйлер доказал, что такого маршрута не существует, а для этого рассмотрел более общий вопрос с любым расположением островов и мостов. Он доказал, что требуемый маршрут существует в том, и только том случае, когда не более чем два острова связаны с внешним миром нечетным количеством мостов. Сегодня мы интерпретируем эту теорему как одну из первых теорем теории графов – науки о сетях из точек, соединенных линиями. Доказательство Эйлера было алгебраическим и использовало символьное представление маршрута, где острова и мосты обозначались буквами. Несложно доказать, что сформулированное Эйлером условие необходимо для существования требуемого маршрута; труднее доказать, что этого достаточно для его существования.

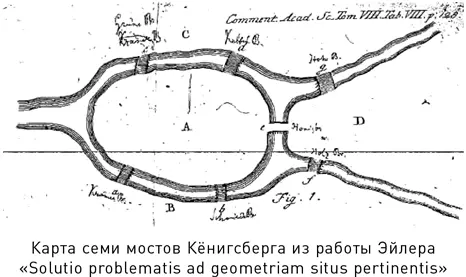
Второй комбинаторной задачей, которую Эйлер поставил в 1782 г., была загадка 36 офицеров. Имеется шесть полков, в каждом из которых есть шесть офицеров шести разных званий. Можно ли построить полки квадратом 6 × 6 так, чтобы ни в одном ряду и ни в одной колонне не оказалось двух офицеров одного полка или одного звания? Эйлер предполагал, что это невозможно, но этому результату пришлось дожидаться доказательства Гастона Тарри до 1901 г. В основе решения здесь лежит латинский квадрат, в котором n экземпляров n символов необходимо разместить в квадрате n × n так, чтобы каждый символ в каждой строке и в каждом столбце встречался ровно один раз. Требуется, чтобы 36 офицеров образовали два «ортогональных» латинских квадрата – один для полка, другой для ранга, так, чтобы все возможные пары были в них включены. Латинские квадраты применяются, в частности, при разработке статистических тестов, а их широкие обобщения, известные как блочные планы, фигурируют в нескольких областях математики. Одна из вариаций на тему такого квадрата – головоломка судоку.

Перечисленные мной результаты едва-едва затрагивают громадный объем всего того, что сделал Эйлер в теоретической математике, но не менее плодовит он был также в прикладной математике и в математической физике.

В своей «Механике» 1736 г. он систематизировал и существенно продвинул искусство расчета движения материальной точки. Самым серьезным новшеством было использование вместо геометрии математического анализа, позволившего унифицировать работу с совершенно разными задачами. За этим последовала книга о кораблестроении, которая начиналась с гидростатики и вводила, кроме того, дифференциальные уравнения для движения твердого недеформируемого тела. Эту тему он развил в 1765 г. в «Теории движении твердых тел», где определил систему координат, известную нынче как Эйлеровы углы; он связал ее с тремя осями инерции тела и моментами его инерции относительно этих осей. Оси инерции – это определенные линии, представляющие особые компоненты вращения тела; соответствующий момент определяет количество вращения относительно выбранной оси. В частности, Эйлер решил свои уравнения для Эйлерова волчка – тела с двумя равноправными осями инерции.

В механике жидкостей Эйлер установил фундаментальные уравнения, ныне известные как уравнения Эйлера, которые не потеряли своего значения до сих пор, несмотря на то что в них не учитывается вязкость. Он изучал теорию потенциала с приложениями в области гравитации, электричества, магнетизма и упругости. Его работа со светом способствовала успеху волновой теории, преобладавшей в физике вплоть до появления в 1900 г. квантовой механики. Некоторые его результаты в небесной механике астроном Тобиас Майер использовал при расчете таблиц движения Луны. В 1740 г. Эйлер написал «Метод нахождения кривых линий» (полное название работы намного длиннее приведенного здесь), где положил начало вариационному исчислению. Его задача – поиск кривых и поверхностей, минимизирующих (или максимизирующих) некоторую связанную с ними величину, такую как длина или площадь. Все его книги понятны, элегантны и прекрасно организованы.

Другие труды Эйлера затрагивают такие темы, как музыка, картография и логика – почти не существует областей математики, которые не привлекли бы внимания Эйлера. Лаплас замечательно сформулировал роль Эйлера: «Читайте Эйлера, читайте Эйлера, он наш общий учитель».

Шел 1804 г., идеи математической физики буквально витали в воздухе. Иоганн Бернулли уже применил Ньютоновы законы движения в комбинации с Гуковым законом о силе, которую развивает растянутая пружина, к колебаниям скрипичной струны. Его идеи привели Жана ле Рона д’Аламбера к формулировке волнового уравнения. Это дифференциальное уравнение в частных производных, описывающее скорости изменения формы струны как в пространстве, так и во времени, показывает поведение самых разных волн – волн на воде, звуковых волн, других колебаний. Аналогичные уравнения в свое время предлагались для магнетизма, электричества и гравитации. Теперь Жозеф Фурье решил применить эти же методы в другой области физики – к потоку теплоты в теплопроводящей среде. После трех лет исследований он представил длинную записку о распространении тепла. Записка была прочитана в Парижском институте и встретила смешанную реакцию, так что решено было организовать комиссию для ее проверки. Когда по итогам проверки был написан отчет, стало ясно, что члены комиссии недовольны. На то у них было две причины – одна хорошая, другая плохая.

Жан-Батист Био обратил внимание членов комиссии на, как он утверждал, проблему с выводом уравнения для потока теплоты. В частности, Фурье не упомянул одну из его собственных работ 1804 г. Это был плохой повод для недовольства, поскольку статья Био была неверна. Хороший же повод состоял в том, что ключевой шаг в рассуждениях Фурье – преобразование периодической функции в бесконечный ряд синусов и косинусов угла, кратного заданному, – не был проведен с должной строгостью. В самом деле, Эйлер и Бернулли не один год пытались обосновать ту же идею в контексте волнового уравнения. Фурье поспешил пояснить свои рассуждения, но комиссию это не удовлетворило.