Карл Левитин - Геометрическая рапсодия

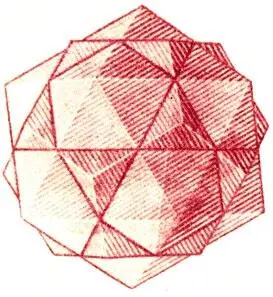
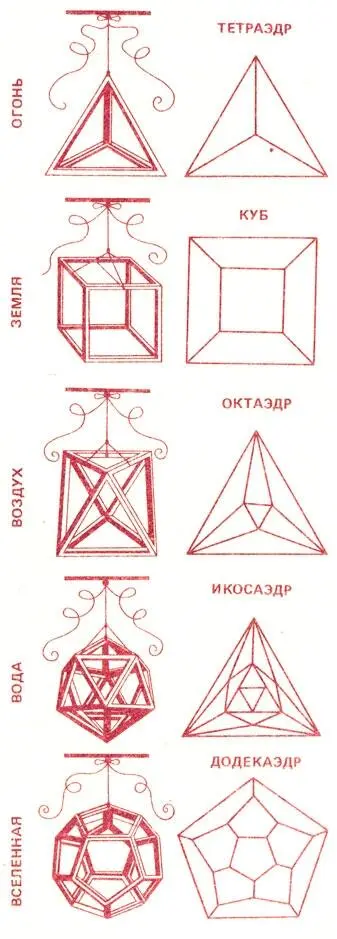
"Греки — это не способные школьники или хорошие студенты, но скорее "коллеги из другого колледжа", — писал профессор Джон Инденсор Литлвуд, один из крупнейших современных английских математиков. Поверим ему и не станем с насмешливым превосходством судить Платона за то, что он считал, будто атомы четырех элементов, из которых строится мир (огня, земли, воздуха и воды), имеют форму правильных выпуклых многогранников — тетраэдра, куба, октаэдра и икосаэдра, а весь мир в целом построен в форме додекаэдра. (На 73-й странице книги пять Платоновых тел сопоставлены с гравюрами Эсхера "Фейерверк", "Итальянский пейзаж. 1923", "Россано, Калабрия", "Второй день творения" и "Другой мир. 1947".) Воздержимся от саркастической улыбки и читая о "пятой сущности", или, по-латыни, "квинтэссенции" алхимиков, хотя их "колледж" чужд нам по духу. Подумаем лучше, почему именно додекаэдр, как показали раскопки в Монте Лоффа под Падуей, был любимой игрушкой этрусских детей 2500 лет назад? И почему он же до наших дней остается излюбленной побрякушкой для взрослых, которые делают из него календарь — по месяцу на каждый из двенадцати его граней (одно из изделий такого рода — брелок для ключей, изготовленный нашим "Автоэкспортом")?

Куб (или гексаэдр) и правильная пирамида (или тетраэдр) тоже верно служили большим и малым людям — и их созидательной тяге к строительству, и их разрушительной страсти азарта. Свидетельство тому — детские кубики и пирамидки, а также вся архитектура конструктивизма. Но почему же не куб и не пирамида, а совсем другой правильный многогранник — икосаэдр — хранится в Египетском зале Британского музея, и удивленный посетитель может узнать, что это — игральная кость династии Птолемеев? И почему октаэдр — "пространственный ромб" — от древних времен до наших дней неизменно служит светильником, хотя "начинка" его прошла путь от скоротечной плошки до почти вечной йодной лампы?

И наконец, главный вопрос: почему Платоновых тел (это математический термин) именно пять? Постарайтесь придумать шестое: выпуклый многогранник, каждая грань которого — один и тот же правильный многоугольник, то есть фигура с равными сторонами и равными углами между ними. Когда попытки ваши кончатся безрезультатно, попробуйте найти способ доказать себе и другим известное любому математику утверждение Евклида: существует только пять правильных выпуклых многогранников. И вне зависимости от успеха этого предприятия вы, вероятно, с большим пониманием, чем прежде, отнесетесь к словам профессора Литлвуда. И вне сомнения, с большим, чем в первый раз, интересом станете рассматривать гравюру Эсхера "Звезды", на которой среди прочих тел легко найти всю нашу "великолепную пятерку".

"Различные ветви геометрии находятся в тесных и часто неожиданных взаимоотношениях друг с другом" — такими словами Давид Гильберт предваряет одну из своих книг. Любой, в том числе и этот, рассказ о геометрии служит подтверждением их правдивости.

Леонардо да Винчи любил изготовлять из дерева каркасные модели многогранников. Когда его друг фра Лука Пачоли издал в 1509 году в Венеции книгу "О божественной пропорции", иллюстрациями к ней послужили пятьдесят девять рисунков, сделанных Леонардо со своих моделей. (Впрочем, Пачоли не остался в долгу: он подсчитал для великого скульптора количество металла, потребного для изготовления статуи всадника, — задача по тем временам нешуточная.)

Что же божественного нашел в простых геометрических фигурах Лука Пачоли — человек, живший спустя два тысячелетия после Платона? Или это отзвук, прошедший через века и народы, приписываемой ему Плутархом крылатой фразы: "Бог всегда действует геометрически"?

Нет, фра Лука — монах Пачоли — мыслил реалистичнее: бог — геометр не всегда, но в некоторых случаях. А именно когда речь идет о "золотом сечении" — о таком делении отрезка на две неравные части, чтобы отношение большей части к меньшей равнялось отношению всего отрезка к большей его части.Завяжите простым узлом узкую полоску бумаги и осторожно распрямите его (12). Вы получите правильный пятиугольник, а его диагонали как раз и делят друг друга "в среднем и крайнем отношении" — так еще по-другому называют "золотое сечение". Пачоли нашел, что есть тринадцать "эффектов" этой "божественной" пропорции — "ради нашего спасения", как утверждал он. Он искал эти "божественные эффекты" в самых совершенных созданиях математики — пяти Платоновых телах, строил их из стеклянных плиток, а затем раздавал "для коллекций разных вельмож". В главе "О двенадцатом, почти сверхъестественном свойстве" речь идет о правильном икосаэдре — платоновом теле, ограниченном двадцатью правильными треугольниками.

Вглядитесь повнимательнее в эту древнейшую игральную кость (13). К каждой вершине сбегаются пять треугольников, свободные стороны которых образуют уже знакомый нам правильный пятиугольник. Если же соединить между собой любые два противоположные ребра икосаэдра, то получится прямоугольник, тоже имеющий прямое отношение к "божественной" пропорции, — его большая сторона так относится к меньшей, как сумма сторон — к большей. И именно икосаэдр связан с математической знаменитостью — проблемой "целующихся сфер", которая возникла в споре Исаака Ньютона с оксфордским астрономом Дэвидом Грегори (4).

Наконец, в самые последние годы это звучное греческое слово вновь замелькало в научных статьях: выяснилось, что структура кристаллического бора — идеальный икосаэдр. И даже вирусы, которые раньше так и назывались "сферическими" — например, вирус полиомиелита, — и то, как удалось обнаружить, имеют форму икосаэдра. Но об этом чуть позже.