Маркос Санчес - Тайна за тремя стенами. Пифагор. Теорема Пифагора

Фрагмент Московского папируса, где излагается задача об усеченной пирамиде.

Имели ли египтяне представление о доказательстве или проверке своих математических действий? Папирус Ринда написан как книга упражнений для учеников того времени, так что некоторые исследователи считают, что хотя Ахмес не сформулировал никаких общих принципов, весьма вероятно, что он их знал. В любом случае, в документе содержатся задачи, которые писец должен был решать в связи с торговыми и административными делами, и методы их решения были практическими правилами, усвоенными опытным путем. Видимо, у египтян не было дедуктивной практики, основанной на системе аксиом.

Получить ясное представление о развитии математики в Древней Индии весьма трудно. С одной стороны, долгое время передача математических и научных знаний в ее культуре происходила в устной форме, с другой — политическая история Индии того периода полна различных событий. Около 4000 года до н.э. на территории нынешней Индии, в бассейне реки Инд, сформировалось классовое общество. Самыми важными городами этой культуры были Хараппа, Мохенджо-Даро, Кот-Диджи и Лотхал. Это были города-государства с развитой торговлей и ремеслами, которые установили торговые отношения с Центральной Азией, Месопотамией и Аравией. До сих пор не удалось расшифровать письменность этих культур, но археологические находки в регионе дают некоторую информацию об уровне математических знаний.

Древние индийцы использовали десятеричную систему счисления. Возможно, они умели пользоваться счетами для числовых операций — так, в Мохенджо-Даро были найдены остатки счетов. Из геометрических фигур они знали квадрат, прямоугольник, треугольник, круг, конус, цилиндр и куб. Нам известно, что они использовали переплетенные круги в качестве геометрического орнамента.

Десятеричная позиционная система и форма написания цифр стали, без сомнения, самым важным вкладом индийских математиков в развитие человечества. Индийская математика всегда использовала десятеричную систему счисления. В санскрите были специальные слова для цифр от 1 до 9 и для числа 10. Развитие этой системы стало возможным благодаря сочетанию двух благоприятных условий, которыми являются устойчивое использование в числовой системе девяти цифр и система традиционных десяток, определяемая систематической шкалой степеней 10. Что касается нуля, весьма важен тот факт, что индийские астрономы знали определенные знаки для пустого количества, свойственные шестидесятеричной вавилонской системе. В VI веке десятеричная система уже была широко распространена, а с VII века используется и ноль, который поначалу представлял собой точку, а затем маленький кружок. Индийцы называли ноль «сунья», то есть «пустой». Арабский перевод этого слова звучит как «аль-сифр», откуда происходит и наша «цифра». Так в названии графического изображения числа содержится отсылка к такому фундаментальному элементу, как ноль.

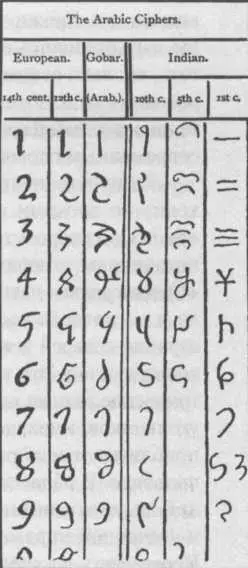
Таблица, показывающая развитие арабских цифр в Европе и в Индии, иллюстрация выполнена британским эрудитом XIX века Исааком Тейлором.

Узоры на вазах и рельефы показывают, что у них были представления о проекциях и подобиях, что они могли делить отрезки пополам и на равные части, разделять круги на две или четыре части и строить отрезки и сегменты окружности, концентрические круги и параллельные прямые. Однако мы не знаем, как они вычисляли площади и объемы элементарных геометрических фигур. С древнейших времен математика была в Индии в большом почете: культ чисел и буддизм находятся в тесной связи. Согласно традиции, Будда научился читать, писать и считать в возрасте примерно восьми лет. Позже, чтобы просить руки своей невесты Ясодхары, ему пришлось выдержать экзамен по математике и сосчитать, сколько атомов в просяном зерне. Для того чтобы найти решение, он изобрел способ расширения числовой последовательности: найденное гигантское число, если его записывать современным способом, равно 384 · 7 13.

Распространение математических знаний в Индии восходит ко времени появления религиозно-философских книг «Веды» во втором тысячелетии до нашей эры. К этим первым источникам относятся и так называемые «правила веревки», «Сулъвасутра», датированная периодом между VIII и II веками до н. э., которая содержит геометрические инструкции по постройке алтарей и использованию для этого веревок и бамбуковых шестов. Эти тексты демонстрируют определенные геометрические знания, среди которых определение площадей многоугольников, имеющее прямое отношение к теореме Пифагора, приблизительные расчеты диагоналей (например, √2) и тому подобное. В области пространственной геометрии древние индийцы умели вычислять приблизительный объем пирамиды и усеченной пирамиды, а также площадь поверхности конуса. Кроме того, в качестве числа π они использовали различные приближения, такие как 27/8 и 243/80.

В первых цивилизациях, в которых получила развитие математика, мы прежде всего находим арифметические действия с целыми числами и дробями, позиционную систему числовой записи, начала алгебры и некоторые полученные опытным путем геометрические формулы. Однако там практически не существовало абстракций и общих методологических принципов или идей о необходимости доказательства для подтверждения правильности операций. Эти народы, таким образом, не знали принципов теоретической науки и не считали математику самостоятельной дисциплиной, достойной изучения именно в качестве таковой. Для них она была только инструментом получения простых правил, который использовался в повседневной жизни лишь для решения конкретных задач.

Переломным периодом для основания математики в ее современном виде стала эпоха Древней Греции. Греческая цивилизация восходит ко второму тысячелетию до н.э. и развивается на территории нынешней Греции и Южной Италии, на севере Африки и в Малой Азии (где, возможно, лежат ее истоки). С самых ранних времен этот народ великих мореплавателей и искателей приключений завязал отношения с египтянами и вавилонянами и, хотя и заимствовал у своих соседей некоторые элементы культуры, сформировал самую оригинальную и могущественную цивилизацию своей эпохи, в долгосрочной перспективе оказавшую огромное влияние на всю западную культуру. Эпоха Древней Греции стала одним из самых блестящих периодов в истории науки.