Маркос Санчес - Тайна за тремя стенами. Пифагор. Теорема Пифагора

Греки (ошибочно) считали египтян изобретателями науки, особенно в области землемерия, астрономии и арифметики. Многие греки ехали в Египет и Вавилон, чтобы изучать эти дисциплины. Такое влияние особенно сильно ощущалось в богатых торговых городах, таких как Милет в Ионии — греческой территории на побережье Малой Азии. В порты Милета прибывали корабли из европейской Греции, из Финикии и Египта, а караванные пути связывали город с Вавилоном. Именно здесь родились философия, математика и вообще большая часть греческой науки.

В дальнейшем классическая греческая математика развивалась в различных городах всего греческого мира, где группы мыслителей собирались вокруг одного мудреца. Получили широкое распространение центры обучения, каждый из которых основывался на опыте своих предшественников. В сущности, это тот же процесс, которому следует наука и в наши дни: когда ведущий ученый приходит в университет или научный центр, вокруг него обычно собирается группа других специалистов и молодых студентов. Ионийская школа была основана Фалесом Милетским, а двумя его учениками были Анаксимандр и Анаксимен. Как уже упоминалось в первой главе, легенда гласит, что Пифагор учился математике у Фалеса.

Фалес Милетский (ок. 630-545 до н.э.) — первый и самый известный из семи мудрецов Греции — этот титул греческая традиция присвоила семи персонажам, жившим в VII—VI веках до н.э. за их мудрость и знания в различных областях науки. На самом деле неизвестно, правда ли Фалес родился в Милете или у него были финикийские корни, как это утверждал Геродот, но его деятельность в Милете в качестве купца и затем законодателя, математика и астронома подтверждается источниками. Часть его торговой деятельности разворачивалась в Египте, где он, по видимости, приобрел некоторые математические познания. Согласно традиции, Фалес предсказал лунное затмение 8 мая 585 года, но, учитывая уровень астрономических знаний того времени, поверить в это трудно. Когда Аристотель наградил его титулом «отца греческой философии», он, вероятно, имел в виду, что Фалес основал ионийскую философскую школу. Без сомнения, вопросы, которые ставил Фалес (например, о сущности вещей и о принципах движения), затрагивали основные темы философии и ознаменовали историческое начало ее зрелого периода.

Бюст, изображающий Фалеса Милетского, Капитолийские музеи, Рим.

Кроме философской деятельности, Фалесу приписывают множество научных свершений, таких как открытие силы притяжения магнита и статического электричества, но особый интерес вызывают его предполагаемые математические результаты. Согласно легенде, во время торгового путешествия в Египет он вычислил высоту пирамид по их теням, которые сравнивал с тенью своего посоха. С помощью принципа подобных треугольников, то есть таких, которые имеют одинаковые углы и пропорциональные стороны, он рассчитал также расстояние от берега до лодки. Но кроме всего прочего, Фалесу приписывают дедуктивные доказательства нескольких знаменитых теорем, которые, согласно традиции, использовались уже давно, но сформулированы и доказаны были только тогда.

Доходило и до утверждений, что именно он сформулировал и доказал саму теорему Пифагора. Как бы то ни было, Фалес дал свое имя двум важнейшим теоремам:

— первая теорема Фалеса: если провести в треугольнике прямую, параллельную любой из его сторон, получившийся треугольник будет подобен заданному (см. рисунок 1);

— вторая теорема Фалеса: если взять точку В, лежащую на окружности с диаметром АС и не совпадающую с А и С утреугольник АВС будет прямоугольным (см. рисунок 2).

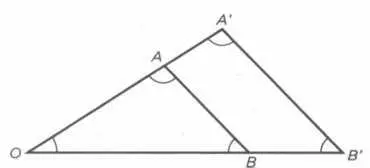
РИС. 1

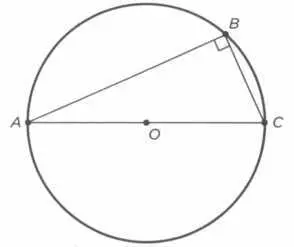
РИС. 2

Однако Фалесу приписывают достижение куда более значительное, чем перечисленные теоремы: считается, что именно он превратил математику в абстрактную науку. В точности подтвердить это мнение невозможно, так как наука в ее современном виде возникла только в XVI веке, в ходе научной революции, однако нет сомнений, что трем великим милетцам — Фалесу, Анаксимандру и Анаксимену — математика обязана первыми своими шагами.

Молчание документальных источников свидетельствует об интеллектуальном бесплодии Ионии со времени смерти философа Анаксимена ок. 524 года до н.э. и до взятия Милета персами в 494 году до н.э. Милетская школа, однако, не исчезла. Великие милетские идеи и открытия оказали огромное влияние на последующих мыслителей, даже если они шли иными путями. Самая близкая в хронологическом смысле к милетской школе фигура — это Пифагор, и действительно, история науки считает, что именно пифагорейцы переняли наследие милетцев. Как было сказано ранее, мы не знаем, что именно мы можем отнести к достижениям Пифагора, а что — к результатам его учеников, так что когда речь заходит о математической деятельности пифагорейцев, на самом деле имеется в виду вклад всей группы вплоть до 400 года до н.э. Из числа пифагорейцев более всего выделяются Филолай (ок. 470-385 до н. э.) и Архит (ок. 435-347 до н. э.).

Математические и геометрические концепции всех доэллинистических цивилизаций были связаны с материей. К примеру, для египтян прямая представлялась натянутой веревкой или бороздой в земле. Первый большой вклад греков в математику — признание того, что математические объекты, числа или геометрические фигуры — это абстракции, идеи, производимые разумом, не связанные с физическими объектами. Тем не менее можно утверждать, что они не всегда придерживались этого взгляда.

Глава V книги I «Метафизики» Аристотеля посвящена в значительной части пифагорейцам и описывает их учение о числах. В сущности, именно на текст Стагирита опираются специалисты при составлении мнения о пифагорейской философии. Указанная глава содержит ясное и точное ее описание, ставшее классическим:

«...так как, далее, они видели, что свойства и соотношения, присущие музыкальной гармонии, выразимы в числах; так как, следовательно, им казалось, что все остальное по своей природе явно уподобляемо числам и что числа — первое во всей природе, то они предположили, что элементы чисел суть элементы всего существующего и что все небо есть гармония и число. И все, что они могли в числах и гармониях показать согласующимся с состояниями и частями неба и со всем мироустроением, они сводили вместе и приводили в согласие друг с другом...»[ 1Перевод А. В. Кубицкого.]