Маркос Санчес - Тайна за тремя стенами. Пифагор. Теорема Пифагора

Еще более священным, чем пятерка, было число 6, символ зарождения и семьи, так как шестерка предполагала союз мужского и женского начал через произведение (6 - 2 · 3). Это число было полно мистики, потому что из него складывались временные интервалы между реинкарнациями. Кроме того, оно представляло площадь божественного треугольника 3-4-5. Но важнее всего было то, что шестерка была первым совершенным числом — об этом типе чисел мы поговорим ниже.

Семерка была « девой без матери», потому что она не могла быть порождена никаким из чисел декады и, в свою очередь, не могла породить никакое из них. Семь ассоциировалось со здоровьем и светом, существовало семь музыкальных нот и семь звезд, давших название дням недели. В геометрическом смысле это число было уникальным, поскольку круг невозможно было разделить на семь равных частей никаким известным построением.

Число 8 символизировало дружбу, полноту и размышление. Значение восьмерки выражалось в ее влиянии на весь космос посредством восьми сфер, которые можно было увидеть с Земли: сферы Луны, Меркурия, Венеры, Солнца, Марса, Юпитера, Сатурна и неподвижных звезд. Это было первое кубическое число (2 3), а его полнота происходила из суммы двух равных квадратов (8 = 4 + 4).

Девятка была символом любви и беременности, так как обычно беременность у женщины длится девять месяцев. Связывали ее и с идеей справедливости, потому что ее множители равны (9 = 3 · 3). Это первый квадрат нечетного числа (3 2).

В этом клянусь тебе Тем, Кто вложил в нашу душу тетрактис, Символ божественной сущности и добродетели высшей!

Клятва пифагорейцев, приведенная в «Золотых стихах»

И наконец, число 10 было символом Бога и Вселенной. Так как первые четыре числа выражали для пифагорейцев тайну музыкального ряда, их сумма (10 =1 + 2 + 3 +4) считалась совершенством, синтезом самой природы числа во всей ее полноте. Математический смысл числа 10 безграничен: оно содержит в себе одинаковое количество чисел четных и нечетных и одинаковое количество составных чисел (4, 6, 8, 9, 10).

Как начало и основа всех вещей, десятка была наивысшим выражением мистической нумерологии пифагорейцев. Ее представляли в виде 10 точек или камешков, сложенных в форме равностороннего треугольника (см. рисунок 5). Эта анаграмма, визуальное и геометрическое представление, получила название «тетрактис декады». Слово тетрактис означает «четверня», что указывает на его строение с основанием 4, и это позволяет понимать тетрактис как «базовая четверка». Тетрактис имел мистический смысл, наподобие пенталъфы, и использовался при произнесении пифагорейской клятвы.

Пифагррейская манера представлять числа с помощью точек или камешков породила их классификацию в соответствии с формой, в которые укладывались эти камешки. Таким образом, «многоугольные числа» ассоциировались с формой правильных многоугольников, что придало им новые свойства.

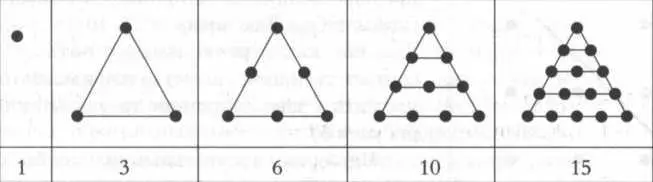
РИС. 5

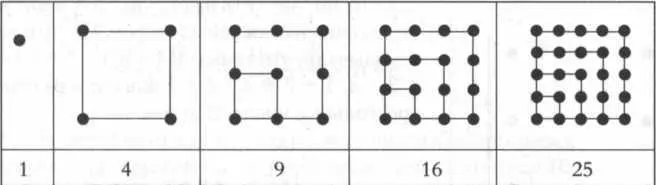
РИС. 6

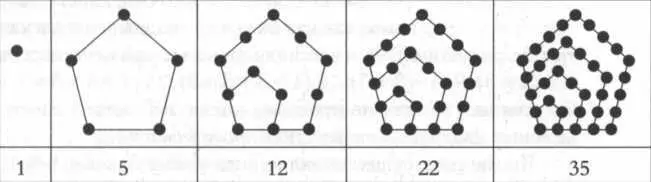
РИС. 7

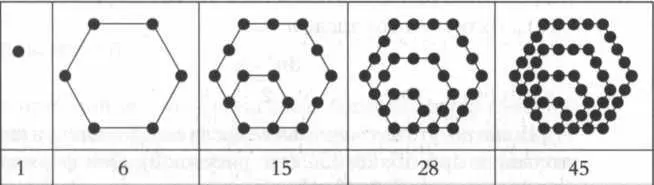
РИС. 8

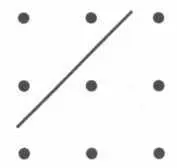
РИС. 9

РИС. 10

Этот вид геометрической алгебры стал предшественником сегодняшней символической алгебры. Так, числа 1, 3, 6, 10, 15... определялись как треугольные, потому что соответственное количество точек можно было уложить в равносторонние треугольники (см. рисунок 5).

Четвертым треугольным числом было сакральное 10, и даже его форма выражала удивительное свойство его «четверности», ведь, как можно заметить на рисунке 5, у него по четыре точки на каждой из сторон. Пифагорейцы показывали, что суммы 1, 1 + 2, 1 + 2 + 3, 1 + 2 + + 3 + 4, 1 + 2 + 3 + 4 + 5 давали в результате треугольные числа. В целом

1 + 2 + ...+ n = n · ((n + 1)/2).

Числа 1, 4, 9, 16, 25... считались квадратными, так как их точки укладывались в квадраты (см. рисунок 6). Они составлялись из серий нечетных чисел:

1.4 (1 + 3), 9 (1 + 3 + 5), 16 (1 + 3 + 5 + 7), 25 (1 + 3 + 5 + 7 + 9)... Составные (то есть не простые) числа, не составлявшие правильных квадратов, назывались продолговатыми.

Кроме того, существовали числа пятиугольные, 1, 5, 12, 22, 35..., которые складывались в пятиугольники (см. рисунок 7). Они формировались из серии 1, 4, 7, 10, 13... таким образом:

1.5 (1 + 4), 12 (1 + 4 + 7), 22 (1 + 4 + 7 + 10), 35 (1 + 4 + 7 + 10 + 13)... Пятиугольное число n:

(3n 2- n)/2.

Понятно, что шестиугольные числа складывались в шестиугольники: 1, 6, 15, 28, 45... (см. рисунок 8). Они формировались из серии 1, 5, 9, 13, 17... следующим путем: 1, 6 (1 +5), 15 (1 + 5 + 9), 28 (1 + 5 + 9 + 13), 45 (1 + 5 + 9 + 13 + 17)... В целом это 2n 2- n.

При таком геометрическом представлении становились заметны некоторые свойства целых чисел. К примеру, если провести прямую внутри квадратного числа, как показано на рисунке 9, становится понятно, что сумма двух последовательных треугольных чисел составляет квадратное число. Можно доказать правильность этого утверждения в целом, хотя и невероятно, чтобы сами пифагорейцы могли прийти к подобному доказательству, которое мы представим в современной нотации:

(n(n+1))/2+((n+1)(n+2)/2) = (n+1) 2

Чтобы перейти от одного квадратного числа к следующему, пифагорейцы следовали схеме, представленной на рисунке 10. Они объединяли точки справа и снизу ломаной под прямым углом линией, которая называлась гномон, что значит «плотницкий угол». Гномон образовывали точки на границе квадрата, количество которых увеличивалось на два с каждым переходом к следующему квадратному числу. Если к любому квадратному числу прибавить его гномон плюс два, мы получим следующее квадратное число. Таким образом, пифагорейцы узнали, что n 2+ (2n + 1) = (n + 1) 2. Кроме того, если, начиная с 1, прибавлять гномон 3, затем гномон 5 и так далее, то получится, что 1 + 3 + 5 + ... + (2n + 1) = n 2.

Пифагорейский мир чисел был очень богат. Пифагор и его последователи различали разные типы чисел, которые они скрупулезно классифицировали и приписывали им нравственные и физические характеристики. К примеру, нечетные числа были мужскими, а четные — женскими. Некоторые числа были дружественными друг другу и сочетаемыми, иные же — зловредными и неспособными к отношениям с другими. Числа могли приносить человеку несчастья. Результатом этой классификации стала запутанная интеллектуальная конструкция, которую можно понять, только встав на позицию пифагорейской мистики. В Книге VII своих «Начал» Евклид попытался объяснить весь этот пифагорейский мир и представить его с максимально возможной ясностью. Категории и определения, приводимые ниже, основаны на данных этого великого геометра.