Маркос Санчес - Тайна за тремя стенами. Пифагор. Теорема Пифагора

1 + 24/60 + 51/60 2 + 10/60 3 = 1, 41421296.

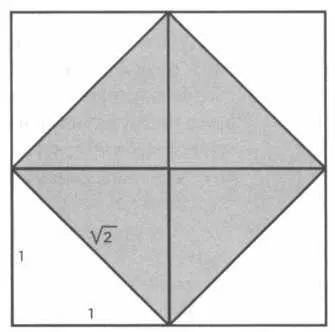
РИС. 1

Как можно увидеть на этой фотографии, исследователи смогли расшифровать клинопись на табличке YBC 7289, хранящейся в Йельском университете.

В индийском трактате «Сульвасутра» значительно более позднего времени (между 800 и 200 годом до н.э.) также можно узнать, что квадрат со стороной 1 и его диагональ не могут быть соизмеримыми. Историки математики интерпретируют следующие слова из книги как приближение √2: «...длина стороны увеличивается на треть, а эта треть на ее четвертую часть, и из этого вычитается тридцать четвертая часть этой четверти». Числовое выражение этой формулы будет таким:

√2 = 1 + 1/3 + 1/(3 · 4) - 1/(3 · 4 · 34) = 577/408 = 1, 414215686.

И все-таки, хотя подобные свидетельства весьма впечатляют, вавилоняне, индийцы и, конечно, египтяне использовали дроби исключительно в практических целях, и это положение не изменилось до развития греческой математики. Вавилоняне не знали, что их шестидесятеричные приближения никогда не будут вполне точными, так же как и египтяне не могли понять саму суть иррациональных чисел. Вопреки намерениям пифагорейцев, их заслуга состояла в открытии, что несоизмеримые соотношения — это нечто совершенно отличное от соизмеримых. Теория пропорций для несоизмеримых соотношений и для любых типов величин была впоследствии выдвинута Евдоксом Книдским (ок. 408-355 до н.э.), философом, математиком и врачом, который был учеником Платона (ок. 427-347 до н.э.).

Невероятные успехи греческой классической цивилизации до сих пор поражают воображение. Несмотря на это, греческая математика оказалась неспособна преодолеть некоторые свои серьезные ограничения, что поставило перед последующими поколениями ряд фундаментальных проблем. В конце концов, то, что было главным достоинством греков — точность концепций и определений, — стало огромным грузом для развития креативной математики.

Арифметика, персонифицированная в лице Боэция и Пифагора, гравюра из «Жемчужины философии», книги Г регора Рейша (1503).

Теорема Пифагора, изложенная в «Атлантическом кодексе» Леонардо да Винчи (Амброзианская библиотека, Милан).

Фрагмент готического рельефа из собора в Шартре с изображением свободных искусств. Фигура слева представляет Пифагора.

Главное ограничение греческой математики, очевидно, состояло в ее неспособности принять идею иррациональных чисел. Это замедлило развитие арифметики и алгебры и вызвало еще большие трудности, поскольку греки в результате свели математику к геометрии, так как геометрические рассуждения не нуждались в таком иррациональном концепте, как число. Из этого проистекало вынужденное разделение числа и величины, в результате которого алгебра и геометрия на долгие века стали восприниматься как дисциплины, не имеющие ничего общего. Кроме того, греческая геометрия была довольно ограниченной. Древние принимали во внимание только те геометрические концепции, которые они могли выстроить в действительности, то есть те, которые могли существовать или быть нарисованы с использованием линейки и циркуля (при этом не допускалось использование линейки с какими-нибудь отметками на ней). Таким образом, геометрия ограничивалась фигурами, которые можно было получить с помощью прямой и круга. Единственными допустимыми поверхностями были те, которые образовывались вращением прямых и кругов вокруг оси, такие как цилиндр, конус и шар, полученные соответственно вращением прямоугольника, треугольника и круга вокруг прямой; призма, являющаяся особой разновидностью цилиндра, или пирамида, которая получается путем разложения призмы. Конические сегменты были результатом сечения конуса плоскостью.

Все эти ограничения, оставляющие в поле зрения строго определенные фигуры, позволили развиться геометрии простой, упорядоченной, гармоничной и красивой, но слишком строгой: утверждая единство, совершенство и простоту и отделяя созерцательную мысль от практической пользы, классическая греческая геометрия ограничивала взгляд математиков, удерживала их разум от новых идей и методов и ставила непреодолимые пределы для новых достижений.

Неспособность принять иррациональные числа как достойные рассмотрения привела к тому, что вопрос числового выражения несоизмеримых соотношений, которым могла бы заняться арифметика, остался открытым. Концепция иррационального числа могла бы расширить и инструментарий алгебры, а вместо этого для решения квадратных или других уравнений приходилось прибегать к геометрии. Все эти задачи могли решаться в числовом виде, и тогда алгебра получила бы развитие по сравнению с тем положением, в котором ее оставили вавилоняне.

Второе ограничение греческой науки состояло в том, что ей так и не удалось осознать понятия бесконечно большого, бесконечно малого и бесконечного процесса. Пифагорейцы связывали добро и зло с ограниченностью и неограниченностью соответственно. Избегая каких-либо заявлений о бесконечности прямой линии, Евклид в «Началах» утверждает, что отрезок при необходимости может быть продлен до нужных пределов. Что касается соотношения между точкой и прямой, то Аристотель настаивал на разделении этих понятий. С одной стороны, он признавал, что точки лежат на прямой, а с другой — утверждал, что непрерывная прямая не может быть образована из дискретных точек.

Даже в области целых чисел и их соотношений у греков не было никакой логической базы: ее заменяли некоторые неточные определения Евклида. Необходимость в логическом фундаменте числовой системы стала, однако, критической, когда александрийцы начали свободнее использовать числа, включая иррациональные.

Таким образом, греки оставили человечеству две отдельные ветви математики: строгую, дедуктивную и систематизированную геометрию и слишком формализованную и эмпирическую арифметику с некоторым продолжением в алгебру. Отсутствие дедуктивной алгебры привело к тому, что всякое упоминание о математической строгости относилось исключительно к геометрии, и эта ситуация сохранялась вплоть до XVII-XVIII веков, когда было положено начало развитию алгебры и математического анализа. Наконец, ограничение евклидовой геометрии фигурами, которые можно построить только с помощью линейки и циркуля, не позволяло математике решить две великие задачи. Первой было разрешение трех проблем, которые в течение веков занимали великие умы и до сих пор привлекают к себе внимание, хотя их решение было найдено в XIX веке: мы говорим о квадратуре круга, трисекции угла и удвоении куба с помощью циркуля и линейки. Вторая задача состояла в расширении критериев существования геометрических фигур, поскольку тот факт, что доказать это существование можно было, лишь построив такую фигуру, сдерживал развитие науки. Кроме того, евклидова прямая не позволяет отложить некоторые длины, и математика, чтобы стать полезной для изучения физического мира, должна была освободиться от этого технического ограничения.