Маркос Санчес - Тайна за тремя стенами. Пифагор. Теорема Пифагора

Таким образом, то, что в современной математике выражается как

√2/2,

есть несоизмеримое соотношение.

История Гиппаса с ее совершенной фабулой, включая драматический финал, сочетает в себе элементы, которым позавидовал бы любой писатель: простой квадрат таит в себе семена разрушения, недальновидный член братства открывает ящик Пандоры... На самом деле не существует доказательств, что эти факты действительно имели место, и невозможно утверждать, что именно Гиппас открыл несоизмеримость квадрата. Еще одна легенда приписывает ему совсем другое доказательство существования несоизмеримости. В истории он остался человеком, который предъявил публике шар, составленный из 12 пятиугольников. Правильный пятиугольник — это математическая фигура, на которой относительно легко продемонстрировать свойство несоизмеримости, особенно с помощью древнего метода бесконечного спуска, который имел фундаментальное для греческой математики значение. С его помощью находили, к примеру, наибольший общий делитель двух чисел.

Метод состоит в следующем: даны две различные величины (a, b), где a < b, и из большей вычиталась меньшая; получалась новая величина b — a, и она вычиталась из a, и так далее. Эта процедура неприменима к паре величин (a и b), если они несоизмеримы. Когда a и b представляют собой натуральные числа, можно определить их наибольший общий делитель (НОД). Данная процедура, называемая евклидовым алгоритмом, всегда конечна и приводит к точному результату. Если процедура бесконечна, то наибольшего общего делителя не существует, и величины несоизмеримы. Эта теорема — мы не будем ее здесь приводить — была доказана Евклидом в книге X «Начал»: «Если даны две величины, и при последовательном вычитании меньшей из большей остаток никогда не сравняется с предыдущей величиной, то эти две величины несоизмеримы ».

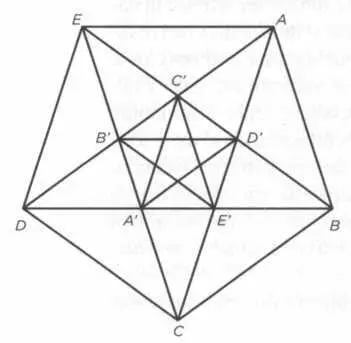
Демонстрация существования несоизмеримых отрезков в пентаграмме.

Как видно на рисунке, диагонали правильного пятиугольника образуют другой правильный пятиугольник и так далее. Для цепочки пятиугольников, получаемых с помощью такого процесса, действительны отношения АЕ =АВ' и B'D =В'Е, где AD - АЕ = В'Е и аналогичным образом АЕ = ED' = ЕА' и В'Е' = B'D = Β'Έ, следовательно, АЕ - Β'Έ' = В'А', и так далее до бесконечности.

Из этого можно вывести, что:

— разница между диагоналями и сторонами большего пятиугольника такая же, как у меньшего пятиугольника;

— разница между сторонами большего пятиугольника и диагоналями меньшего равна сторонам меньшего пятиугольника;

— разница между диагоналями меньшего пятиугольника и его сторонами снова равна диагоналям следующего меньшего треугольника и так далее.

Эта процедура бесконечного спуска никогда не завершится, и, соответственно, невозможно найти наибольшую общую величину для диагоналей и сторон правильного пятиугольника, следовательно, взаимно несоизмеримые отрезки существуют.

Некоторые исследования показывают, что доказательство несоизмеримости стороны и диагонали квадрата относится к более позднему времени, чем эпоха пифагорейцев, так как оно более изощренное, чем метод бесконечного спуска. Квадрат с его диагоналями лишь потом позволили констатировать наблюдение, уже замеченное в других примерах, таких как пентаграмма.

В книге X «Начал» Евклид берется за задачу классификации иррациональных чисел по типам: в этом тексте содержится 115 предложений, хотя наиболее древние издания добавляют к ним предложения 116 и 117. Это последнее представляет доказательство иррациональности на основе теоремы о четных и нечетных числах с применением теоремы Пифагора, где оно излагается так же, как и в наше время во многих книгах на эту тему.

По словам Евклида, согласно теореме Пифагора, в равнобедренном прямоугольном треугольнике квадрат гипотенузы равен удвоенному квадрату каждого из катетов. Если длину катета считать за 1, какой будет длина гипотенузы?

Предположим, что ее длина составляет т/п метров:

m2/n2 = 2

Предположим m и n не имеют общего делителя и делятся друг на друга, тогда m или n должно быть нечетным. Так как m 2= 2n 2, то m 2четное и, следовательно, m тоже четное, то есть n — нечетное. Таким образом, мы можем подставить m = 2p. Следовательно, 4p 2= 2n 2; из этого выводится, что n 2= 2p 2, и значит, n четное. Выходит, что никакая дробь вида m/n не может выражать длину гипотенузы. Это соображение подчеркивает, что при любой единице измерения есть такие длины, которые не могут быть выражены числовым соотношением на основе этой единицы, в том смысле что не существует таких целых чисел тип, чтобы взятая т раз длина совпадала с взятой п раз единицей измерения. Метод Евклида используется и сегодня для доказательства иррациональности √2, однако ученые склонны считать, что он был добавлен в текст «Начал» значительно позже. В современных изданиях Евклида этот метод обычно опускается, и книга X оканчивается предложением 115.

Как мы уже говорили, введение иррациональных чисел определило независимость геометрии от арифметики. В книге II «Начал» Евклид геометрическим методом доказывает многие вещи, которые сегодня доказываются алгебраически, к примеру (a + b) 2= a 2+ 2ab + b 2. К этому его вынуждала проблема несоизмеримых величин, и пока не была найдена арифметическая теория, пригодная для операции с подобными числами, геометрический метод Евклида оставался для этого наиболее удобным.

√2 был первым открытым иррациональным числом, научным успехом величайшей важности, который на века определил задачи математики в области вещественных чисел. Хотя история Гиппаса, по-видимому, показывает нам величественную картину краха пифагорейской Вселенной, найти √2 несложно — сложно понять, что с ним делать. Чтобы обнаружить его, достаточно нарисовать на листе квадрат, как это сделано на рисунке 1. Главный квадрат делится на четыре маленьких со стороной 1, а затем проводятся их диагонали. Таким образом мы получаем внутренний квадрат с площадью 2, который занимает половину квадрата со стороной 2. Сторона этого внутреннего квадрата, умноженная на себя, будет равна 2. Таким образом, мы получили квадратный корень из двух, или, в современной нотации, √2. Нарисовав эту фигуру на бумаге, уже невозможно смотреть на месопотамскую табличку, хранящуюся в Йельском университете под номером YBC 7289, без некоторого изумления. Эта находка датируется периодом между 1800 и 1600 годом до н.э. и на ней изображен квадрат с двумя диагоналями, которые с легкостью позволяют найти √2. Рисунок сопровождается семью цифрами, нацарапанными клинописью по вавилонской шестидесятеричной системе. Исследователи утверждают, что эти числа соответствуют приближению √2 в первых знаках после запятой: