Маркос Санчес - Тайна за тремя стенами. Пифагор. Теорема Пифагора
- Название:Тайна за тремя стенами. Пифагор. Теорема Пифагора
- Автор:
- Жанр:
- Издательство:Де Агостини
- Год:2014
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Маркос Санчес - Тайна за тремя стенами. Пифагор. Теорема Пифагора краткое содержание
Тайна за тремя стенами. Пифагор. Теорема Пифагора - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
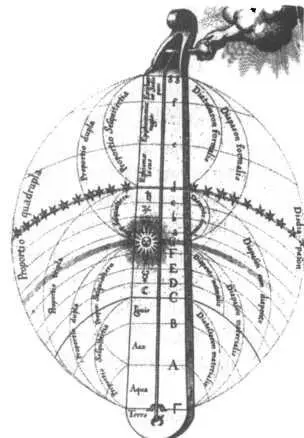
Знаменитый рисунок монохорда из трактата Anatomiae Amphitheatrum.
Наиболее наглядный пример такой слепоты — греческая космология. Уже в III веке до н.э. стало понятно, что круговые орбиты не соответствуют наблюдаемым движениям небесных тел. Тогда в модель были введены эпициклы — маленькие круги, центр которых движется по основной орбите. Со временем число эпициклов росло, система усложнялась и стала совершенно бесполезной. Сама мысль о том, что небесные тела движутся по каким-то другим, не круговым орбитам, древними греками даже не рассматривалась: это должен быть именно круг — совершенная фигура.
Даже Николай Коперник (1473-1543) в своем великом труде De revolutionibus orbium celestium («О вращении небесных тел»), опубликованном в год его смерти, переместил Землю из центра Вселенной и заменил ее Солнцем, но остался верен круговым орбитам. Только в 1609 году Иоганн Кеплер (1571— 1630) предположил, что орбиты на самом деле эллиптические. Но даже этот революционер не смог полностью избавиться от влияния поэтической идеи о музыкальной гармонии космоса. Хотя Кеплер был ключевой фигурой для научной революции, этот великий немецкий астроном и математик оставался мистиком. Тридцать лет своей жизни он потратил на то, чтобы доказать, что движение планет подчиняется пифагорейским законам гармонии. В поисках фундаментального закона, объясняющего неправильность планетных орбит, Кеплер измерил для каждой планеты ее максимальную скорость в перигелии (ближайшей к Солнцу точке орбиты) и в афелии (самой дальней от Солнца точке). К радости ученого, соотношения между двумя этими скоростями соответствовали гармоническим интервалам, и поэтому он обозначил эти соотношения символами музыкальной нотации, отдав таким образом дань пифагорейской идее музыки сфер. Кеплер изложил свою теорию в трактате Harmonia mundi («Гармония мира»), вышедшем в 1619 году. На его страницах он представил гамму и аккорды, связанные с каждой из планет. Согласно автору, планеты исключительно редко звучат все вместе в совершенном согласии, такая симфония может сложиться только один раз за всю историю мира с момента его сотворения.
ГЛАВА 6
Крах универсальной арифметики
Пифагорейская картина совершенного музыкального космоса, основанная на священном числе, столкнулась с большой проблемой: это число должно быть целым. Хотя дроби были уже известны, греческая арифметика игнорировала их. Однако сама теорема Пифагора несла в себе зерна разрушения, и чтобы они проросли, надо было всего лишь произвести некоторые простые, но фатальные расчеты. Появление иррациональных чисел означало крах пифагорейской универсальной арифметики.
Нельзя утверждать, что пифагорейцы не имели никакого представления о дробях. Последователи самосского мудреца использовали эквивалентную дробям концепцию соотношений между целыми числами, которые позволяли им, к примеру, объяснять звуковую гармонию двух струн, выражая ее в отношениях их длин: 2:1, 3:2, 4:3... Дроби были известны математике еще со времен Месопотамии, где они использовались в повседневной жизни — например, в торговле для обозначения частей денежных единиц. Но при всем этом во времена пифагорейцев математики считали дроби чем-то несовершенным и бесполезным.

Может быть точно установлено, как две величины, А и В, соотносятся друг с другом, с использованием только целых чисел.
На рисунке верхняя строка длиннее нижней, а нижняя — в 13/20 раза короче верхней.
Самое прочное убеждение последователей Пифагора, опора их арифметической вселенной, состояло в том, что любые две величины всегда соизмеримы, то есть их всегда можно сопоставить с двумя целыми числами. Принцип соизмеримости относится к тому, что сегодня называют рациональными числами. Рациональное число — это число, которое можно представить как дробь, то есть отношение, или коэффициент, между двумя целыми числами (при этом делитель не должен быть равен нулю). Пифагорова соизмеримость может быть представлена как закон, согласно которому точно устанавливается, во сколько раз величины А и В больше (или меньше) одна другой. В современных математических терминах мы бы сказали, что две произвольные величины А и В соизмеримы тогда, когда существует третья величина С и два целых числа р и q, так чтобы С укладывалось р раз в А и q раз — в В.
Современная математика определяет число как элемент множества, который обладает некоторыми свойствами. Так, существуют множества N, Z, Q, R и С, которые представляют собой последовательные ступени, начиная с множества натуральных чисел N.
| С Комплексные | R Вещественные | Q Рациональные | Z Целые | N Натуральные | Простые |
| Составные | |||||
| 0 Ноль | |||||
| Целые отрицательные | |||||
| Дробные | |||||
| Иррациональные | |||||
| Мнимые |
— Комплексные (С): сумма вещественного и мнимого чисел.
— Вещественные (R): совокупность рациональных и иррациональных чисел.
• Рациональные (Q): числа, которые могут быть представлены как одно целое число, деленное на другое целое число (а точнее, на натуральное положительное число), то есть как дробь общего вида т/п с числителем т и знаменателем п, отличным от нуля. Термин «рациональные» происходит от латинского ratio («соотношение»).
• Иррациональные: числа, которые не могут быть выражены дробью вида т/п, где т и п представляют целые числа и п отлично от нуля, или для которых дробь является бесконечной, как, например, 3, 1415... (π), 2, 7182... (е), 1, 6180... (Ф) или 1, 4142135... (√2). Всякое вещественное число, не являющееся рациональным, иррационально.
— Мнимые: комплексные числа с нулевой вещественной частью, к примеру 5/ (где / = VI1). Это число вида z = х + /у, где х = 0.
В группе рациональных чисел выделяют:
— целые (Z): совокупность чисел, которые включают натуральные числа, отличные от нуля, отрицательные числа и ноль;
— натуральные (N): любое число, которое может служить для счета. Это числа 1, 2, 3, 4...;
— ноль: числовой знак с пустым значением, который в позиционной записи занимает место, где нет никакой значимой цифры;
— целые отрицательные: вещественные числа меньше нуля. Противоположностью отрицательного числа является число положительное, и наоборот. Единственное число, одновременно и положительное, и отрицательное, — это ноль;
Читать дальшеИнтервал:
Закладка:









