Маркос Санчес - Тайна за тремя стенами. Пифагор. Теорема Пифагора

— дробные: числа, которые представляют собой одну величину, деленную на другую.

В пределах группы натуральных чисел различаются:

— простые числа: числа больше 1, которые делятся только на себя и на 1. Например, простыми числами являются 2, 3, 5, 7, 11, 13, 17, 19, 23... 2 — это единственное четное простое число;

— составные числа: любое натуральное не простое число, кроме 1 и О, которые имеют 1 и более делителей, отличных от 1 и от них самих. Они называются также делимыми. К таким числам относятся, например, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18...

Но идеальный мир, где все так прекрасно подогнано друг к другу, не мог выдержать натиска реальности. Парадоксальным образом простые вычисления на основе именно теоремы Пифагора могли свести на нет всю эту стройную конструкцию. И так как именно пифагорейцы были наиболее продвинутыми математиками своей эпохи, это был лишь вопрос времени — кто из них первым выполнит губительные вычисления.

Математик и философ Гиппас родился около 500 года до н.э. в городе Метапонте в Тарентском заливе, Южная Италия. Дата его смерти неизвестна, и на этом, вероятно, строится легенда, связанная с ним. Кроме несоизмеримости, математику приписывают два важных открытия: применение додекаэдра в качестве приближения шара и открытие числовых соотношений основных музыкальных аккордов путем экспериментов со звуком.

Есть надежные свидетельства о том, что Гиппас ставил акустические опыты и изучал резонанс, поэтому его считают теоретиком музыки. Согласно легенде, он не только доказал существование иррациональных чисел, но и нарушил пифагорейский закон молчания, поведав о своем открытии миру. Дошедшие до нас документы того времени приводят различные версии его смерти, но ни одну из них нельзя считать достоверной.

Практически установлено, что математическое открытие существования отрезков, взаимно несравнимых, то есть несоизмеримых, произошло в пифагорейской школе не позднее чем в 420 году до н.э. Так как пифагорейцы весьма интересовались тройками целых чисел, которые могли представлять соотношения сторон прямоугольного треугольника, понятно, что они должны были открыть эти новые соотношения, хотя некоторые исследования указывают и на другие возможности, о которых мы поговорим позже. Как правило, исследования по истории математики согласны с традицией, которая приписывает обескураживающее открытие иррациональных чисел Гиппасу из Метапонта. По одной из версий, в качестве наказания за то, что он ввел в мир элемент, не отвечающий основополагающему принципу секты, — что все явления Вселенной могут быть сведены к целым числам и их отношениям, — члены братства сбросили Гиппаса с борта корабля. На самом деле мы не знаем в точности, каким образом были открыты иррациональные числа. Традиция гласит также, что Гиппас изучал свойства квадрата. Хотя это и весьма простая фигура, пифагорейцы не знали никого, кому удалось бы вычислить ее диагональ: это удалось сделать Гиппасу с помощью теоремы Пифагора. В поисках универсального доказательства этот математик смог вычислить диагональ, приняв сторону квадрата за 1. Далее следовала простая операция: оставалось разбить квадрат на два треугольника и применить теорему Пифагора для вычисления их гипотенузы (см. рисунок). В равнобедренном прямоугольном треугольнике квадрат гипотенузы равен удвоенному квадрату катета. Если длину катетов принять за 1, какой будет длина гипотенузы? Полученное число не будет ни целым, ни дробью... Оно будет несоизмеримым. В современной математической терминологии мы бы сказали, что прямоугольный треугольник с катетами, равными 1, имеет гипотенузу длиной √2, и это иррациональное число. Но во времена Гиппаса это открытие потрясало основы пифагорейской философии.

Этот результат не только показывал, что гипотенуза равнобедренного прямоугольного треугольника несоизмерима с катетами, но и поставил греческую математику перед фундаментальной проблемой.

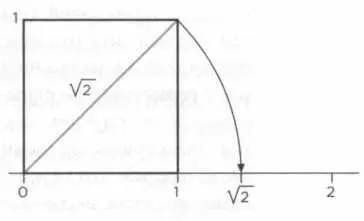
Графическое представление доказательства Гиппаса из Метапонта. Математик из Великой Греции вычислил диагональ квадрата — величину, до тех пор неизвестную, — использовав теорему Пифагора.

Пифагорейцы постулировали абсолютную связь между числом и геометрией, но существование несоизмеримых величин подрывало сами основы этих отношений. Конечно, из-за этого члены братства не перестали изучать длины и соотношения в геометрии, но ограничились числовыми соотношениями только в тех случаях, когда они были соизмеримы. Со временем геометрические величины дистанцировались от величин числовых, так что те и другие стали изучаться раздельно. Введение понятия несоизмеримости убедило греческих математиков в том, что геометрия должна развиваться независимо от арифметики. Так разрушалась пифагорейская традиция, которая не делала различия между этими областями знания. Из «Диалогов» Платона ясно видно, что уже в его время геометрия считалась отдельной наукой.

Каким образом пифагорейцы так поздно заметили этот слабый пункт, который привел к кризису их систему? Что они ожидали найти в диагонали квадрата? Согласно теореме Пифагора, для квадрата со стороной 1 построенный на его диагонали квадрат будет иметь площадь, равную 2, и, таким образом, длина d данной диагонали должна быть числом, которое при возведении в квадрат дает 2 (то есть (d2 = 2). Здесь на сцену возвращается √2. Величина √2 была длиной отрезка, который можно, опираясь на квадрат, легко построить с помощью линейки и циркуля. Естественным было и предположение, что введя некую величину u (меньшую 1), можно было ею одновременно измерить и сторону (1), и диагональ (√2) квадрата? Очевидным было предположение, что сторона и диагональ квадрата должны быть соизмеримы. Однако это оказалось не так.

Такая постановка задачи приводит к следующему выводу: при умножении общей единицы и на некое целое число п должна получиться длина стороны 1 = nu, а при умножении ее на другое целое число m получается длина диагонали √2 = mu. Следовательно, должно быть верно следующее:

Иными словами, соизмеримость предполагает, что √2 представляет собой дробь вида m/n, где m и n — целые положительные числа. Идя по этому пути, пифагорейцы столкнулись с весьма неприятным результатом: они выяснили, что существуют числа, которые невозможно выразить через отношение целых чисел, и это открытие было несовместимо с их идеей универсальной арифметики. Последователи учителя назвали соизмеримыми соотношениями те, которые можно было выразить целыми числами, что означало, что обе величины могли быть измерены некоей общей единицей, а остальные — несоизмеримыми соотношениями.