Эдвард Шейнерман - Путеводитель для влюбленных в математику

Мы просто решили поиграть и сами придумали правила. Хорошо, теперь давайте поразмышляем. Посмотрим, на что годно это число i . Мы знаем, что i × i = –1. А как насчет i + i ? Если следовать привычным арифметическим правилам, то получится другое мнимое число: 2 i . А что, если возвести это число в квадрат? Попробуем!

(2 i ) ² = (2 i ) × (2 i ) = 2 × i × 2 × i = 2 × 2 × i × i = 4 × ( i × i ) = 4 × (–1) = –4.

Другими словами, число 2i представляет собой квадратный корень из числа –4.

Теперь возведем в квадрат 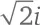и посмотрим, что получится:

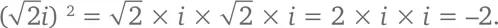
Таким образом, 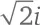представляет собой квадратный корень из числа –2. Когда мы приютили мнимое число i в семье всех чисел, мы заполучили не просто 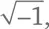а в придачу еще и квадратные корни из всех отрицательных действительных чисел! Любое число вида b × i , где b – это действительное число, называют мнимым числом.

Если сложить два мнимых числа, например 2i и 4i , мы получим другое мнимое число: 6i . Если мы перемножим два мнимых числа, например 3i и –2i , то получим действительное число:

3 i × (–2 i ) = 3 × (–2) × i × i = (–6) × (–1) = 6.

Чтобы мнимые числа прижились в семье всех чисел, нужно научиться складывать, вычитать, умножать и делить мнимые и действительные числа вместе. Мы будем работать с множеством комплексных чисел . Это расширение множества действительных чисел, включающее все числа вида a + bi , где a и b – действительные числа, например 3 + 4 i .

Само число i комплексное, потому что может быть представлено в виде 0 + 1 i . Точно так же действительные числа могут быть представлены в виде –7 + 0 i .

Складывать комплексные числа несложно, мы просто приводим подобные слагаемые:

(3 + 2 i ) + (4 – 3 i ) = (3 + 4) + (2 – 3) i = 7 – i .

Более педантично мы можем записать это так: 7 + (–1) i .

Вычитание ничуть не сложнее:

(3 + 2 i ) – (4 – 3 i ) = (3 – 4) + (2 – (–3)) i = –1 + 5 i .

Очевидно, что сумма или разность двух комплексных чисел – тоже комплексное число. На языке алгебры мы можем продублировать эту фразу так (числа a, b, c, d здесь – действительные):

( a + bi ) + ( c + di ) = ( a + c ) + ( b + d ) i ;

( a + bi ) – ( c + di ) = ( a – c ) + ( b – d ) i .

Умножение комплексных чисел дается несколько труднее. Попробуем перемножить наших друзей 3 + 2 i и 4 – 3 i :

(3 + 2 i ) × (4 – 3 i ) = 3 × (4 – 3 i ) + 2 i × (4 – 3 i ) = (3 × 4 – 3 × 3 i ) + (2 i × 4 – 2 i × 3 i ) = (12 – 9 i ) + (8 i + 6) = 18 – i .

На алгебраическом языке произведение двух комплексных чисел выражает формула:

( a + bi ) × ( c + di ) = ( ac – bd ) + ( ad + bc ) i .

Очевидно, что при перемножении двух комплексных чисел мы получаем комплексное число.

Из всех арифметических операций деление комплексных чисел сложнее всего. Оно приводит нас к выражению ( a + bi ) / ( c + di ), поэтому сначала нам придется поговорить о взаимно обратных числах. Число x называют взаимно обратным числу y , если xy = 1. Например, дробь 1/2 взаимно обратна числу 2.

Какое комплексное число взаимно обратно 1 + 2 i ? Нам нужно такое число a + bi , что (1 + 2 i ) × ( a + bi ) = 1. Докажем, что этому требованию удовлетворяет число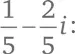

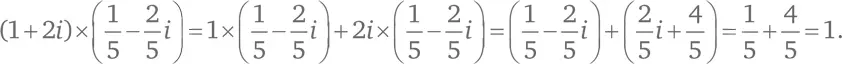
Общая формула для комплексного числа, обратного числу a + bi , выглядит следующим образом:

В этом легко убедиться: достаточно умножить (A) на a + bi , аккуратно произвести все необходимые арифметические действия – и получить в итоге единицу.

Заметим, что оба знаменателя в (A) равны a ² + b ². Если вдруг эта сумма окажется равной нулю, формула потеряет смысл, потому что деление на ноль запрещено. Но такое возможно лишь в том случае, если a = 0 и b = 0 . Другими словами, все комплексные числа имеют взаимно обратные, кроме числа 0 + 0 i . Это подтверждает ожидания: ноль – единственное действительное число, не имеющее взаимно обратного, и среди комплексных чисел дело обстоит так же. Но обратное по отношению к любому ненулевому комплексному числу – тоже комплексное число.

Расправившись со взаимно обратными числами, мы можем наконец перейти к делению. Деление числа X на число Y дает такой же результат, как умножение числа X на число, взаимно обратное Y . Следовательно, частное двух комплексных чисел (если делитель не равен нулю) – комплексное число.

Отсюда можно сделать вывод: основные арифметические действия – сложение, вычитание, умножение и деление – прекрасно справляются с комплексными числами. Мы можем проделать эти операции над парой любых комплексных чисел (исключение составляет деление на ноль) и получить комплексное число.

Сейчас мы снова попытаемся извлечь квадратный корень. Сперва именно эта задача загнала нас в тупик. Действительные числа, так сказать, неполноценны: из каких-то квадратный корень извлекается, а из каких-то – нет. И вот мы дополняем действительные числа мнимыми, придумав новое число 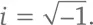Мы заново осваиваем арифметические операции, и система действительных чисел разрастается до системы комплексных чисел [58] Строго говоря, в системе действительных чисел должны выполняться соотношения порядка, аксиомы сложения и умножения и свойство полноты. Однако все эти выкладки, конечно, слишком сложны для научно-популярного обзора. – Прим. пер. . Но как решить вопрос с квадратным корнем? Чему равен 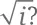Нам что, опять нужно изобрести какое-то несуществующее число и создать монструозное множество «сверхкомплексных» чисел?

К счастью, множество комплексных чисел уже содержит все квадратные корни из комплексных чисел. Посмотрим, как извлечь корень из мнимой единицы, не создавая новых сущностей.

Нам нужно найти такое комплексное число a + bi , что ( a + bi ) ² = i . Начнем с перемножения ( a + bi ) и ( a + bi ):