Эдвард Шейнерман - Путеводитель для влюбленных в математику
- Название:Путеводитель для влюбленных в математику
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2018
- Город:Москва
- ISBN:978-5-9167-1131-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Эдвард Шейнерман - Путеводитель для влюбленных в математику краткое содержание
Путеводитель для влюбленных в математику - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
( a + bi ) × ( a + bi ) = ( a ² – b ²) + (2 ab ) i .
Теперь нам нужно приравнять это выражение к i = 0 + 1 × i . В результате мы получим: a ² – b ² = 0 и 2 ab = 1.
Первое условие тождественно тому, что a = b или a = – b .
Если a = b и 2 ab = 1, то 2 a ² = 1.
Таким образом, 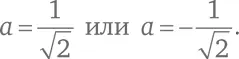
Так как a = b , мы нашли два квадратных корня из мнимой единицы:
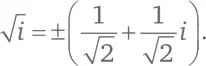
Проверьте, так ли это, возведя оба ответа в квадрат.
Если a = – b , решение будет таким же.
Итак, затратив некоторые усилия, мы показали, что извлечение квадратного корня из комплексного числа дает комплексное число, поэтому придумывать новые числа для извлечения корней не нужно.
А как насчет кубических корней? Кубический корень из числа c – это такое число x , что x ³ = c . Вопрос: входит ли множество корней из комплексных чисел во множество комплексных чисел или нам нужно изобретать еще какие-нибудь новые числа [59] Вот вам испытание: найдите все кубические корни из i .
?
Уравнение x ³ = c может быть записано иначе: x ³ – c = 0. Сформулируем вопрос в общем виде: всякое ли полиномиальное уравнение [60] То есть уравнение вида c 0 + c 1 x 1 + … + c m x m = 0. – Прим. пер.
имеет решение среди комплексных чисел? Скажем, есть ли такое комплексное число x , что
3 x ⁵ + (2 – i ) x ⁴ + (4 + i ) x ³ + x – 2 i = 0?
Принципиально важный факт в теории комплексных чисел состоит в том, что любое полиномиальное уравнение имеет комплексное решение! Об этом говорит основная теорема алгебры. На математическом языке данный тезис можно переформулировать так: поле комплексных чисел [61] На языке математики поле – это такое множество, для элементов которого заданы операции сложения и умножения, обладающие набором определенных свойств (так называемые аксиомы поля). Через них можно определить вычитание и деление. Все эти операции не должны выводить за границы данного множества. – Прим. пер.
алгебраически замкнуто .
Вот как звучит это важнейшее утверждение в строгой форме.
Теорема(основная теорема алгебры). Пусть d – положительное целое число и c 0, c 1, c 2, …, c d – комплексные числа, причем c d ≠ 0. Тогда существует такое комплексное число z, что
c dz d+ c d – 1 z d – 1+ … + c 2 z ² + c 1 z + c 0= 0.
Поле действительных чисел незамкнуто, потому что среди действительных чисел не всегда можно найти решение полиномиального уравнения с действительными коэффициентами (например, среди действительных чисел нет такого числа a , что a × a + 1 = 0. Доказательство общей теоремы алгебры состоит в том, что решение приведенного выше полиномиального уравнение находят в общем виде.
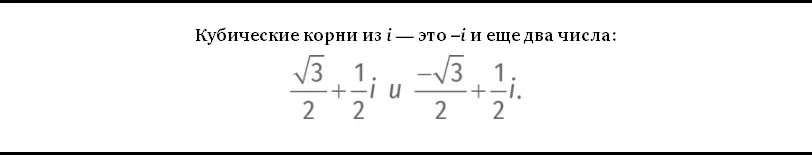
Глава 6
π
Число π завораживает человечество на протяжении многих поколений. Оно проникло в массовую культуру (например, стало названием фильма [62] «π» – триллер 1998 года, режиссер Даррен Аронофски. Главный герой фильма занимается теорией чисел. – Прим. пер.
и маркой одеколона [63] Имеется в виду одеколон Pi Givenchy. – Прим. пер.
). Школьники отмечают День π и соревнуются, кто запомнит больше знаков числа π после запятой [64] День π отмечают 14 марта (3.14), потому что π ≈ 3,14.
.
Пи – шестнадцатая буква греческого алфавита. В математике ею обозначают отношение длины окружности к ее диаметру. Длина окружности в π раз длиннее диаметра, или C = πd . Можно записать иначе: C = 2 πr , где r – радиус окружности.
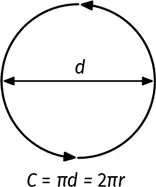
Площадь окружности можно вычислить по формуле S = πr ².
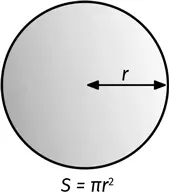
С помощью числа π можно определить и площадь сферы – 4 πr ², а также объем шара – 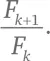
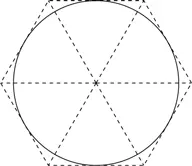
Эти геометрические формулы не сообщают нам величину числа π . Начнем с того, что π больше 3. Нарисуем круг с радиусом 1, впишем в него равносторонний шестиугольник, а затем поделим его на равносторонние треугольники.
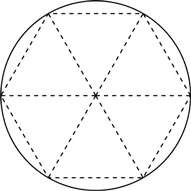
Очевидно, что стороны всех треугольников равны 1. Периметр шестиугольника равен 6. Длина окружности несколько больше, чем периметр шестиугольника. Таким образом, 2 π > 6, следовательно, π > 3. На рисунке мы видим, что разница между периметрами двух фигур невелика. Значит, π немногим больше 3.
Дальше мы можем поступить наоборот – описать правильный шестиугольник вокруг окружности радиусом 1. Вновь поделим шестиугольник на шесть равных треугольников. Длина любой стороны каждого треугольника будет равна 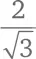 (вы с легкостью поймете, почему это так, применив теорему Пифагора, о которой идет речь в главе 14; объяснение вы найдете в конце главы).
(вы с легкостью поймете, почему это так, применив теорему Пифагора, о которой идет речь в главе 14; объяснение вы найдете в конце главы).
Таким образом, периметр большого шестиугольника равен 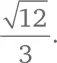 Периметр окружности немного меньше. Следовательно,
Периметр окружности немного меньше. Следовательно,
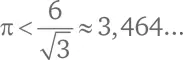
Дальше мы можем снова и снова вписывать в окружность и описывать вокруг нее правильные многоугольники со все бо́льшим количеством сторон. Когда мы дойдем до правильного 100-угольника, точность наших вычислений значительно повысится:
3,1410759… < π < 3,1426266…
В пределе, увеличивая число сторон вписанных и описанных правильных многоугольников до бесконечности, мы будем получать все более точное значение интересующего нас числа:
π = 3,141592653589793238462643383279502884…
Так чему же в точности равно число π ? В главе 4 мы уже выяснили, что число 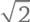 иррационально, то есть не может быть выражено через отношение двух целых чисел. Так же обстоит дело и с числом π . Школьников часто просят запомнить, что
иррационально, то есть не может быть выражено через отношение двух целых чисел. Так же обстоит дело и с числом π . Школьников часто просят запомнить, что 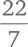 но это лишь приблизительное значение
но это лишь приблизительное значение [65] Дробь Другое соотношение ближе к истине:
.
Интервал:
Закладка:










