Эдвард Шейнерман - Путеводитель для влюбленных в математику

Ae rt,

где e – знакомое нам число Эйлера. В нашем примере A = 1000 (первоначальный вклад), r = 0,1 (процентная ставка), t = 10 (количество лет). В конце мы имеем 2718,28 доллара.

Процесс может быть и обратным, когда нечто непрерывно убывает [74] Экспоненциальная убыль встречается в природе. Пример – радиоактивный распад атомов. . Тогда в конце мы получим Ae – rt .

В одном городе был театр. Его посетители на время представления сдавали шляпы в гардероб, а потом забирали обратно.

Однажды гардеробщик – то ли он выпил лишнего, то ли просто свихнулся – стал выдавать шляпы не по номеркам, а в произвольном порядке. Вопрос: какова вероятность того, что никто не получит свою шляпу?

Сформулируем вопрос точнее. В театр пришло N зрителей. Они встают в очередь за шляпами. Сумасшедший гардеробщик выдает шляпы в произвольном порядке. Таким образом, шляпы могут быть выданы N ! различными вариантами [75] Восклицательный знак означает факториал. Подробнее о факториале вы можете прочесть в главе 10. . Все они равновероятны. Это математическая формулировка выражения «в произвольном порядке».

Разберем случай N = 4. Укажем в таблице все варианты выдачи шляп и пометим стрелочкой те случаи, когда ни один из зрителей не получает свою шляпу.

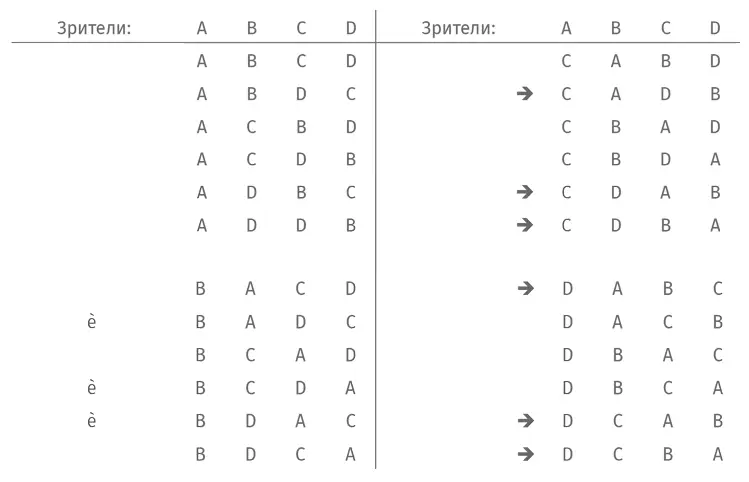
В 9 случаях из 24 никто не получает свою шляпу. Таким образом, при N = 4 интересующая нас вероятность равна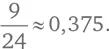

Для N = 5 существует 5! = 120 различных вариантов вернуть шляпы. Из них 44 нам подходят: ни один человек не получит свою шляпу. Таким образом, вероятность будет равна 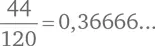В таблице вы можете видеть, как меняется вероятность по мере возрастания N .

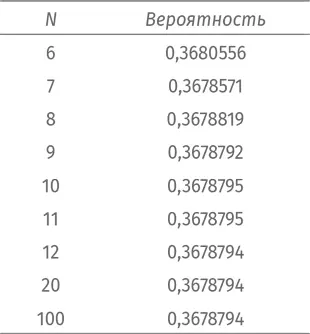
Вероятность меняется и дальше, но на ничтожно малую величину.

Хорошенько подумав, мы можем вывести формулу зависимости вероятности того, что никто из N зрителей не получит свою шляпу, от числа N :

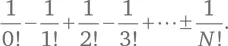
Например, при N = 4

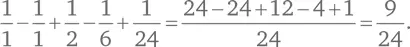
Это согласуется с нашими предыдущими выкладками.

В пределе, когда N стремится к бесконечности, вероятность того, что никто не получит свою шляпу, равна

Этот ряд уходит в бесконечность. Обратите внимание, что эта формула похожа на формулу (A) для подсчета числа e . Сумма ряда (B) равна 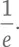Мы снова встретили наше заветное число!

Уже при N = 10 сумма ряда будет равна

Это достаточно близко к следующему значению:

В главе 1 я доказал, что простых чисел бесконечно много. Вы увидели, что среди небольших целых положительных чисел простые числа встречаются достаточно часто, но, когда мы уходим в бесконечность, простые числа начинают попадаться все реже. Мы можем с некоторой точностью установить, насколько редко встречаются простые числа, если попытаемся найти среднее расстояние между ними [76] Примечание для тех, кто знаком с логарифмами: для того чтобы выяснить, насколько редко встречаются простые числа, когда мы рассматриваем большие величины, можно посчитать количество простых чисел между 1 и каким-нибудь крупным числом N . Важнейший результат в теории чисел показывает, что чем больше N , тем ближе количество простых чисел между 1 и N к величине где ln N – логарифм числа N по основанию e , или натуральный логарифм N . Этот результат зафиксирован в так называемой теореме о распределении простых чисел. .

Какие простые числа можно найти между 1 и 20?

2, 3, 5, 7, 11, 13, 17, 19.

Промежутки (разности) между этими числами следующие:

1, 2, 2, 4, 2, 4, 2.

Следовательно, среднее расстояние между ними равно:

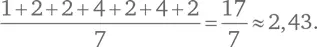
Теперь посчитаем, сколько простых чисел между 1 и 1000. Всего их 168: начиная с 2, 3 и 5 и заканчивая 983, 991 и 997. Среднее расстояние между соседними простыми числами в этом случае составит:

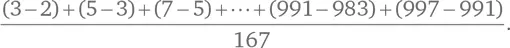
Знаменатель равен 167, так как простых чисел 168, а промежутков между ними на 1 меньше. Числитель можно посчитать довольно просто. Обратите внимание, что число 3 встречается дважды с разными знаками. Та же история с числом 5. Разумеется, это верно для всех чисел, кроме первого и последнего [77] Числитель в этом выражении – пример телескопического ряда, где все слагаемые взаимно уничтожаются. Представьте себе складной телескоп, состоящий из нескольких частей. Точно так же слагаемые телескопического ряда вкладываются друг в друга. . Таким образом, нам достаточно вычесть 2 из 997. Получается, что среднее расстояние между простыми числами от 1 до 1000 равно

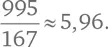
Это в два с лишним раза больше, чем в случае, когда мы брали числовой ряд от 1 до 20.

Введем обозначение agap( N ) для среднего расстояния между простыми числами от 1 до N . Тогда наши предыдущие расчеты могут быть записаны в таком виде:

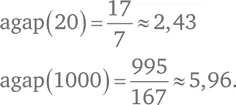
Вычислим среднее расстояние между простыми числами от 1 до N , когда N равно 100, 1000, 10 000 и так далее до 1 000 000 000. И округлим результат до тысячных:

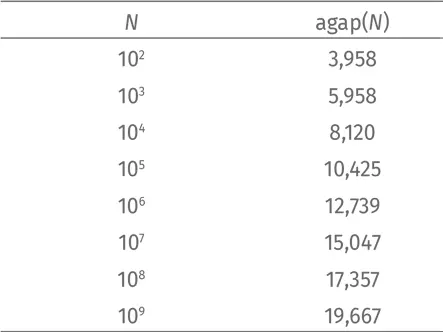
Легко заметить: когда N становится больше в десять раз, agap( N ) возрастает примерно на 2,3.