Эдвард Шейнерман - Путеводитель для влюбленных в математику

1 ↔ 3,

2 ↔ 8,

5 ↔ 11.

Впрочем, когда элементов мало, поиски взаимно однозначного соответствия обременительны и не приносят большой пользы.

Разберем более запутанный пример. Представьте себе, что в некоторый клуб входит семь человек (для удобства будем называть их по номерам: 1, 2, 3, …, 7).

Клубу разрешили послать трех членов на ежегодную национальную конференцию. Есть много способов выбрать трех человек из семи. Пусть A – множество всех возможных групп по три человека:

A = {123, 124, 125, …, 567}.

Здесь мы под «123» подразумеваем, что на конференцию поедут члены клуба под номерами 1, 2 и 3.

На следующий год членов клуба оповещают, что они могут отправить на конференцию четырех человек. Пусть B – множество всех групп по четыре человека:

B = {1234, 1235, 1236, …, 4567}.

Итак, A – множество групп по три человека, B – множество групп по четыре человека.

Совпадают ли их мощности?

Если внимательно пересчитать все элементы, выяснится, что мощности этих множеств совпадают. Но выписывать все возможности одну за одной – нудная и не застрахованная от ошибок работа [83] Нам не обязательно знать все элементы |A| или |B|, чтобы констатировать, что |A| = |B|. .

Гораздо проще показать, что эти множества равновелики, если найти взаимно однозначное соответствие между их элементами. В голову приходит следующая мысль. Допустим, члены клуба решают, что на вторую конференцию больше не поедут те, кто побывал там в первый год. Тогда каждую группу по три человека из первого множества можно сопоставить с другой группой по четыре человека из второго множества. Например, если 1, 4 и 5 поехали на конференцию в первый год, то на следующий год поедут 2, 3, 6 и 7. Или: 145 ↔ 2367.

Выпишем все возможности:

123 ↔ 4567

124 ↔ 3567

125 ↔ 3467

…

356 ↔ 1257

…

567 ↔ 1234

Это взаимно однозначное соответствие показывает, что A и B равновелики.

Вы можете выписать все элементы множеств полностью и убедиться, что их количество совпадает (хотя взаимно однозначное соответствие избавляет нас от этой нудной работы). Перечень всех элементов вы найдете в конце главы.

Подытожим: у нас есть два способа доказать, что конечные множества имеют равные мощности: пересчитать их элементы или найти между ними взаимно однозначное соответствие. Однако, если множество содержит бесконечно много элементов, первый метод перестает работать: ни одно число не подходит на роль мощности ℝ (множество действительных чисел). Таким образом, нам остается лишь найти взаимно однозначное соответствие, чтобы показать, что мощности двух бесконечных множеств совпадают. Вот пример.

Как мы помним, буквой ℤ обозначается множество целых чисел:

ℤ = {…, –3, –2, –1, 0, 1, 2, 3, …}.

Введем обозначение ℤ +для множества положительных целых чисел [84] Это множество натуральных чисел, его обычно обозначают ℕ. – Прим. науч. ред. :

ℤ += {1, 2, 3, 4, …}.

Совпадают ли мощности ℤ и ℤ +?

Есть искушение сказать, что ℤ содержит вдвое больше элементов, чем ℤ +и потому «в два раза более бесконечно». Однако мощности данных множеств совпадают. Почему? Мы покажем это с помощью взаимно однозначного соответствия.

Составим два перечня. Первый будет включать все положительные целые числа, а второй – вообще все целые числа, и положительные, и отрицательные, но в необычном порядке. Сопоставляя числа в первом и втором перечне, мы выстроим взаимно однозначное соответствие. Это показано в таблице [85] Вот две задачки. Какое число будет стоять справа на сотой строке перечня? Какое число слева будет соответствовать числам 100 и –100 справа? Ответ – в конце главы. .

Таким образом, мощности ℤ и ℤ +равны, что, в принципе, и неудивительно – ведь оба эти множества бесконечны.

Выстроив взаимно однозначное соответствие между элементами двух множеств, мы показали, что мощности ℤ и ℤ +совпадают, что они, так сказать, «одинаково бесконечны». Пришло время для вопроса поинтереснее: совпадают ли мощности ℤ +и ℝ? Да, разумеется, оба бесконечны. Впрочем, лучше не утверждать наверняка, пока мы не выстроим взаимно однозначное соответствие между их элементами. Сейчас мы убедимся, что это невозможно.

Итак, мы должны сопоставить каждый элемент первого множества с элементом второго множества и убедиться, что каждый элемент второго множества сопоставлен с элементом первого. Как же доказать, что это невозможно? Мы покажем, что попытки выстроить все элементы ℤ +и ℝ в пары обречены на провал, потому что кое-какие элементы ℝ окажутся пропущены. А теперь к делу!

Допустим, мы все-таки нашли взаимно однозначное соответствие между ℤ +и ℝ. Тогда все элементы можно занести в таблицу такого рода:

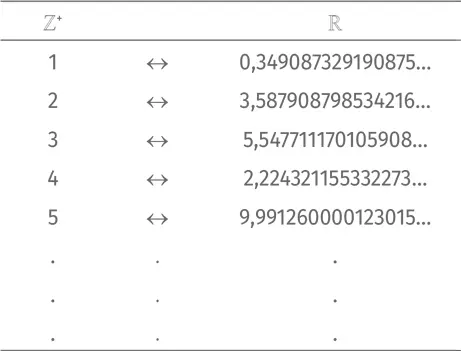
Все целые положительные числа занесены в левую колонку, все (вроде бы) действительные числа занесены в правую колонку. Сейчас мы убедимся: как ни заполняй правую колонку, будут действительные числа, которые туда не попадут.

Но прежде нам придется отвлечься на одну досадную техническую проблему [86] При первом чтении главы эти два абзаца можно пропустить. Мы уточняем одну техническую деталь, чтобы сделать аргументацию полной и неуязвимой. . Некоторые действительные числа в десятичной системе счисления записываются двумя способами. Например, число 1/4. С одной стороны, мы можем записать его как 0,25. С другой стороны, можно записать и так: 0,24999999999999… Ряд девяток уходит в бесконечность. 0,25 тоже можно записать с бесконечным количеством нулей на конце. Таким образом,

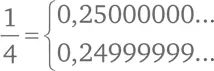
Примем решение вносить в таблицу запись числа с нулями на конце. Это никак не влияет на доказательство, мы просто договариваемся о форме записи.

Итак, вернемся к доказательству. Представим, что перед нами уже лежит таблица с колонками целых положительных и действительных чисел. Поищем действительное число, ускользнувшее из правой колонки.

Для начала подчеркнем первую цифру после запятой в первой колонке, вторую цифру после запятой во второй колонке и т. д.:

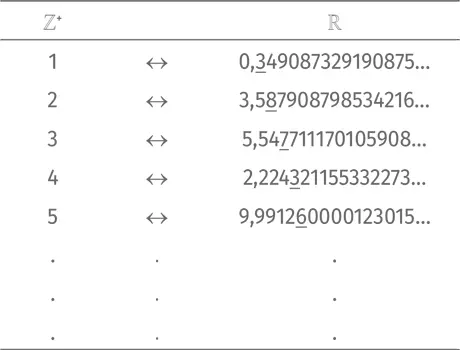
Выпишем подчеркнутые цифры в ряд: 3, 8, 7, 3, 6… С помощью этого ряда создадим новое число. Начнем его с нуля, поставим десятичную запятую и дальше будем двигаться по ряду подчеркнутых цифр с двумя условиями: