Эдвард Шейнерман - Путеводитель для влюбленных в математику
- Название:Путеводитель для влюбленных в математику
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2018
- Город:Москва
- ISBN:978-5-9167-1131-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Эдвард Шейнерман - Путеводитель для влюбленных в математику краткое содержание
Путеводитель для влюбленных в математику - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
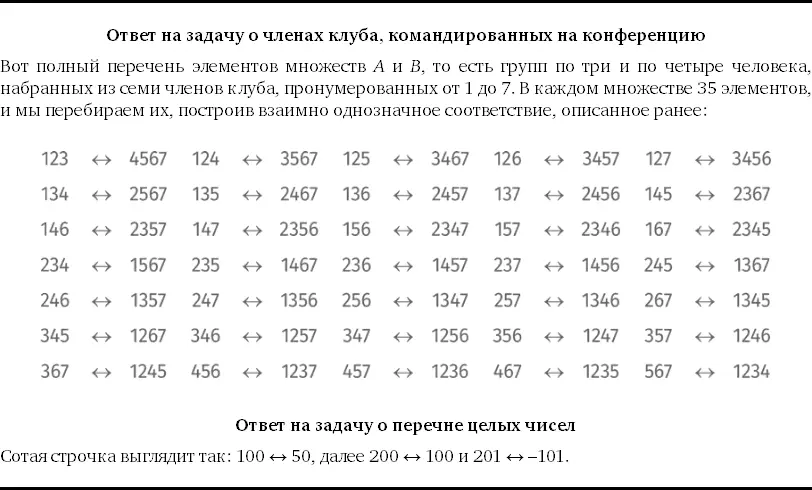
Глава 9
Числа Фибоначчи [95] Эта глава повествует о знаменитых числах Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21 и т. д. Этот ряд был назван в честь Леонардо Пизанского, больше известного как Фибоначчи. (Леонардо Пизанский (1170–1250) – один из первых крупных математиков средневековой Европы. Прозвище Фибоначчи означает «сын Боначчи». Автор «Книги абака», излагающей десятичную систему счисления. – Прим. пер. )
Начнем с укладки квадратов и домино. Вообразим длинную горизонтальную рамку размерами 1 × 10. Мы хотим полностью заполнить ее квадратами 1 × 1 и костяшками домино 1 × 2, не оставив ни единой щели. Вот картинка:
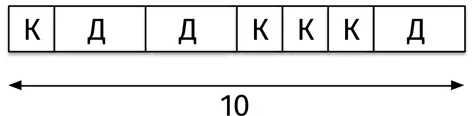
Вопрос: сколькими способами это можно сделать?
Для удобства обозначим число вариантов F 10. Перебирать их все и потом пересчитывать – тяжелый труд, чреватый ошибками. Гораздо лучше упростить задачу.
Не будем с места в карьер искать F 10, начнем с F 1. Это проще простого! Нам нужно заполнить рамку 1 × 1 квадратами 1 × 1 и костяшками домино 1 × 2. Домино не поместится, остается единственное решение: взять один квадрат. Другими словами, F 1= 1.
Теперь разберемся с F 2. Размер рамки 1 × 2. Можно заполнить ее двумя квадратами или одной костяшкой домино. Таким образом, есть два варианта, и F 2= 2.
Дальше: сколькими способами можно заполнить рамку 1 × 3? Первый вариант: три квадрата. Два других варианта: одна костяшка домино (две не влезут) и квадрат слева или справа. Итак, F 3= 3.
Еще один шаг: возьмем рамку 1 × 4. На рисунке показаны все варианты заполнения:
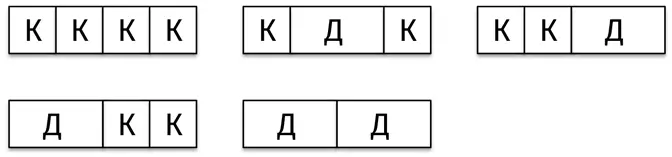
Мы нашли пять возможностей, но где гарантия, что мы ничего не упустили? Есть способ проверить себя.
В левом конце рамки может быть или квадрат, или костяшка домино. В верхнем ряду на рисунке – варианты, когда слева квадрат, в нижнем ряду – когда слева домино.
Допустим, слева квадрат. Оставшуюся часть нужно заполнить квадратами и домино. Другими словами, нужно заполнить рамку 1 × 3. Это дает 3 варианта, так как F 3= 3.
Если слева домино, размер оставшейся части 1 × 2, и заполнить ее можно двумя вариантами, так как F 2= 2.
Таким образом, у нас есть 3 + 2 = 5 вариантов, и мы удостоверились, что F 4= 5.
Теперь ваша очередь. Подумайте пару минут и найдите все варианты заполнения для рамки 1 × 5. Их немного. Решение – в конце главы. Можете отвлечься и подумать.
Вернемся к нашим квадратам. Хочется верить, что вы нашли 8 вариантов, так как есть 5 способов укладки, где слева квадрат, и еще 3 способа, где слева домино. Таким образом, F 5= 8.
Подытожим. Мы обозначили F N количество способов заполнения рамки 1 × n квадратами и костяшками домино. Нам необходимо найти F 10. Вот что мы уже знаем:
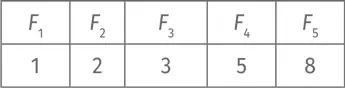
Двигаемся дальше. Чему равно F 6? Можно нарисовать все варианты, но это скучно. Лучше разобьем вопрос на две части. Сколькими способами можно заполнить рамку 1 × 6, если слева (a) квадрат и (b) костяшка домино? Хорошая новость: мы уже знаем ответ!
В первом случае нам остается пять квадратов, а мы знаем, что F 5= 8. Во втором случае нужно заполнить четыре квадрата; нам известно, что F 4= 5. Таким образом, F 5+ F 4= 13.
Чему равно F 7? Исходя из тех же соображений, F 7= F 6+ F 5= 13 + 8 = 21. А как насчет F 8? Очевидно, F 8= F 7+ F 6= 21 + 13 = 34. И так далее. Мы обнаружили следующую взаимосвязь:
F n = F n – 1+ F n – 2.
Еще несколько шагов – и мы найдем искомое число F 10. Правильный ответ – в конце главы.
Числа Фибоначчи – это последовательность:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
Она выстраивается по таким правилам:
– первые два числа 1 и 1;
– каждое следующее число получаем сложением двух предыдущих.
Будем обозначать n-ный элемент последовательности F n , начиная с нуля:
F 0= 1, F 1= 1, F 2= 2, F 3 = 3 , F 4 = 5, …
Очередной элемент мы вычисляем по формуле:
F n = F n – 1+ F n – 2.
Как мы видим, задача об укладке квадратов и домино привела нас к последовательности чисел Фибоначчи [96] В задаче о квадратах и домино мы выяснили: F 1 = 1, а F 2 = 2. Но числа Фибоначчи начинаются с F 0 = 1. Как это согласуется с условиями задачи? Сколько существует способов заполнить на тех же условиях рамку 0 × 1? Длина квадрата и длина костяшки домино, как ни крути, больше нуля, потому есть искушение сказать, что ответ равен нулю, но это не так. Прямоугольник 0 × 1 уже заполнен, там нет щелей; нам не понадобится ни квадрат, ни костяшка домино. Таким образом, есть всего один способ действия: не брать ни квадрата, ни костяшки домино. Понимаете? В таком случае я вас поздравляю. У вас душа математика!
.
Попробуем сложить первые несколько чисел Фибоначчи. Что мы можем сказать о сумме F 0+ F 1+ … + F n для любого n ? Давайте проделаем кое-какие вычисления и посмотрим, что получится.
Обратите внимание на результаты сложения внизу. Видите ли вы закономерность? Повремените немного, прежде чем двигаться дальше: будет лучше, если вы найдете ответ самостоятельно, а не прочтете уже готовое решение.

Хочется верить, вы увидели, что результаты суммирования, если к ним приплюсовать по единице, тоже выстраиваются в последовательность чисел Фибоначчи. Например, сложение чисел от F 0до F 5дает:
F 0+ F 1+ F 2+ F 3+ F 4+ F 5= 1 + 1 + 2 + 3 + 5 + 8 = 20 = F 7 – 1.
Сложение чисел от F 0до F 6дает 33, что на единицу меньше F 8= 34. Мы можем записать формулу для неотрицательных целых чисел n :
F 0+ F 1+ F 2+ … + F n = F n + 2–1. (*)
Вероятно, лично вам достаточно будет увидеть, что формула (*) работает в дюжине случаев, чтобы вы поверили, что она верна, но математики жаждут доказательств. Мы рады представить вам два возможных доказательства того, что она верна для всех неотрицательных целых чисел n . Первое называется доказательством по индукции , второе – комбинаторным доказательством .
Формула (*) представляет собой бесконечно много формул в свернутом виде. Доказать, что (*) верно для конкретного значения n , скажем для n = 6, – простая арифметическая задача. Достаточно будет записать числа от F 0до F 6и сложить их:
Читать дальшеИнтервал:
Закладка:










