Эдвард Шейнерман - Путеводитель для влюбленных в математику
- Название:Путеводитель для влюбленных в математику
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2018
- Город:Москва
- ISBN:978-5-9167-1131-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Эдвард Шейнерман - Путеводитель для влюбленных в математику краткое содержание
Путеводитель для влюбленных в математику - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Сколько вариантов в каждой колонке?
В первой колонке – пять вариантов. Если отбросить домино слева, мы получим ровно F 4= 5 вариантов для прямоугольника 1 × 4.
Во второй колонке – три варианта. Отбросим домино и квадрат слева. Мы получим F 3= 3 варианта для прямоугольника 1 × 3.
Аналогично для других колонок. Вот что мы обнаружили:

Таким образом, количество способов замостить квадратами и домино (хотя бы одной костяшкой) прямоугольную рамку 1 × 6 равно
F 4+ F 3+ F 2+ F 1+ F 0= 12.
Вывод:
F 0+ F 1+ F 2+ F 3+ F 4= 12 = F 6 – 1.
Рассмотрим общий случай. Нам дана рамка длиной n + 2. Сколько есть вариантов ее заполнения, при которых первая костяшка домино находится на некой позиции k ? В этом случае первые k – 1 позиций заняты квадратами. Таким образом, в общей сложности занята k + 1 позиция [99] Число k может принимать значения от 1 до n + 1, но не больше, потому что иначе последняя костяшка домино высунется за пределы рамки.
. Оставшиеся ( n + 2) – ( k + 1) = n – k + 1 можно заполнить любыми способами. Это дает F n – k + 1вариантов. Построим диаграмму:

Если k меняется от 1 до n + 1, величина n – k + 1 меняется от 0 до n . Таким образом, количество вариантов заполнения нашей рамки с использованием хотя бы одной костяшки домино равно
F n + F n – 1+ … + F 1+ F 0.
Если поставить слагаемые в обратном порядке, мы получим левую часть выражения (*). Таким образом, мы нашли второй ответ на поставленный вопрос:
F 0+ F 1+ … + F n .
Итак, у нас есть два ответа на вопрос. Величины, полученные с помощью двух выведенных нами формул, совпадают, и тождество (*) доказано.
Сложение двух следующих друг за другом чисел Фибоначчи дает очередное число Фибоначчи. В этом разделе мы затронем вопрос поинтереснее: что будет, если мы поделим число Фибоначчи на предшествующее ему в ряду? Посчитаем соотношение 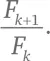 Для возрастающих значений k . В таблице вы можете видеть соотношения от
Для возрастающих значений k . В таблице вы можете видеть соотношения от 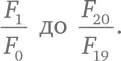

Чем больше становятся числа Фибоначчи, тем ближе соотношение 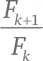 к константе, примерно равной 1,61803.
к константе, примерно равной 1,61803.
Это число – вы будете удивлены – достаточно известное, и если вы введете его в поисковую систему, вывалится уйма страниц о золотом сечении . Что это такое?
Соотношение соседних чисел Фибоначчи не одинаково. Однако оно почти одинаково, если числа достаточно велики. Давайте найдем формулу для числа 1,61803 и для этого на время будем считать, что все соотношения одинаковы. Введем обозначение x :
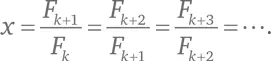
Это значит, что F k + 1= xF k, F k + 2= xF k + 1и т. д. Можно переформулировать:
F k + 2= xF k + 1= x ² F k .
Но мы же знаем, что F k + 2= F k + 1+ F k . Таким образом,
x ² F k = xF k + F k .
Если мы поделим обе части на F k и перегруппируем слагаемые, то получим квадратное уравнение:
x ² – x – 1 = 0.
Оно имеет два решения:
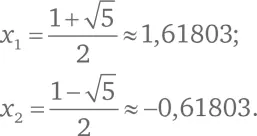
Соотношение должно быть положительным. И вот мы получили знакомое нам число. Обычно для обозначения золотого сечения используют греческую букву ϕ (фи):
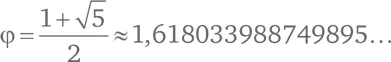
Мы уже приметили, что соотношение соседних чисел Фибоначчи приближается (стремится) к ϕ. Это замечательно. Это дает нам еще один способ вычислять приблизительные значения чисел Фибоначчи.
Последовательность чисел Фибоначчи – это ряд F 0, F 1, F 2, F 3 , F 4, F 5…Если все соотношения 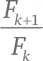 будут одинаковы, мы получим формулу:
будут одинаковы, мы получим формулу:
F n = c ϕ ⁿ .
Здесь с – еще одна константа. Сравним округленные значения F n и ϕ ⁿ для разных n :
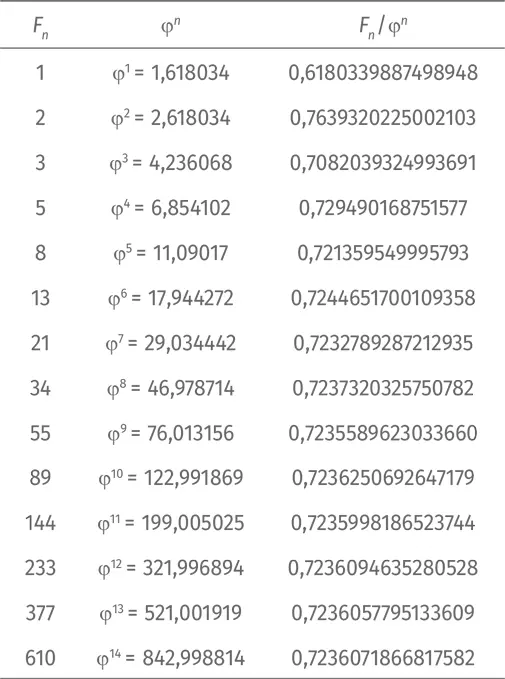
Для больших значений n соотношение 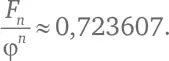 Это число равно в точности
Это число равно в точности 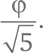 Другими словами,
Другими словами,
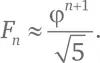
Насколько хороша эта формула? Настало время новых подсчетов!

Обратите внимание: если округлить 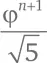 до ближайшего целого числа, мы получим в точности F n .
до ближайшего целого числа, мы получим в точности F n .
Если вы не хотите утруждать себя округлениями до целого числа, то формула, названная в честь Жака Бине [100] Жак Бинe (1786–1856) – французский математик, механик и астроном. Формула для чисел Фибоначчи названа в честь Бине, хотя почти на сто лет раньше ее вывел Абрахам де Муавр (1667–1754). – Прим. пер.
, даст вам точное значение:
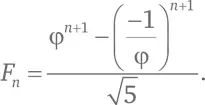

Глава 10
Факториал!
Сколькими способами можно расставить ваши книги на полке? Разумеется, это зависит от того, сколько у вас книг. Начнем с простейшего примера. Допустим, ваша библиотека насчитывает всего три книги с незамысловатыми названиями A, B и C.
Вначале решим, какую книгу поставить с левого края. Пусть это будет A. В таком случае остается всего два варианта расположения книг на полке: ABC и ACB. То есть, когда A стоит слева, существует две комбинации.
Если поставить на левую позицию книгу B, тогда снова возможны два варианта: BAC и BCA. Если слева стоит книга C, появляются еще две комбинации: CAB и CBA.
Читать дальшеИнтервал:
Закладка:










