Эдвард Шейнерман - Путеводитель для влюбленных в математику

Закон Бенфорда утверждает нечто большее, чем «единица на первой значащей позиции встречается чаще всего, а девятка – реже всего». Закон Бенфорда констатирует (при наличии большого количества данных) следующую частотность [111] Мы приводим округленные значения. На самом деле ожидаемая частотность для 1 составляет 30,102999566398114…%. Скоро мы растолкуем, откуда берется это значение. :

Есть и другая область, где обнаруживается неравномерное распределение первых значащих цифр, – это знакомая всем таблица умножения [112] Обычно таблица умножения включает 10 строк и 10 столбцов, но умножение на 10 в нашем случае ничем не отличается от умножения на 1, поэтому один столбец мы выпускаем. :

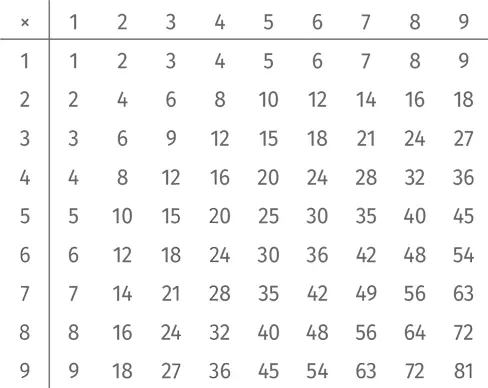
Среди 81 числа в этой таблице 18 начинаются на 1, а именно:

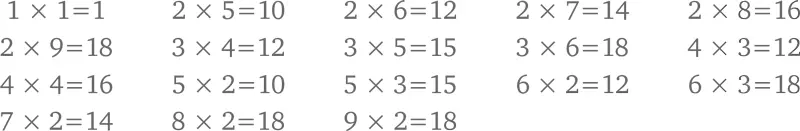
При этом всего 3 числа начинаются на 9:

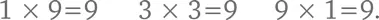
Вот процентное соотношение первых значащих цифр в обычной таблице умножения.

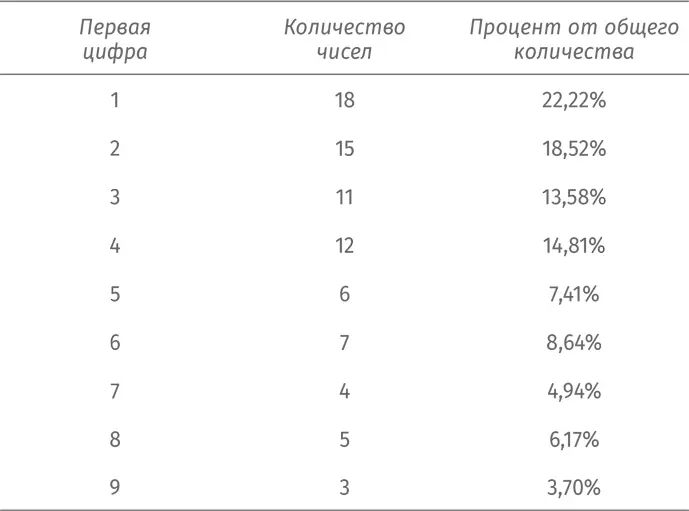
Мы видим, что цифры поменьше встречаются чаще, чем цифры побольше, но частотность здесь не совсем такая, какую предсказывает закон Бенфорда.

Таблица умножения дает нам все возможные результаты умножения одного однозначного числа на другое от 1 × 1 до 9 × 9.

Давайте расширим этот принцип и переберем все варианты умножения трех однозначных чисел. Проделаем следующие вычисления [113] Можно наглядно увидеть трехмерную таблицу умножения на примере кубика Рубика. Некоторые варианты (например, 4 × 7 × 3 = 84) будут скрыты внутри кубика. :

В общей сложности это дает 9³ = 729 троек. Посмотрим, как часто встречаются разные цифры в первой позиции:

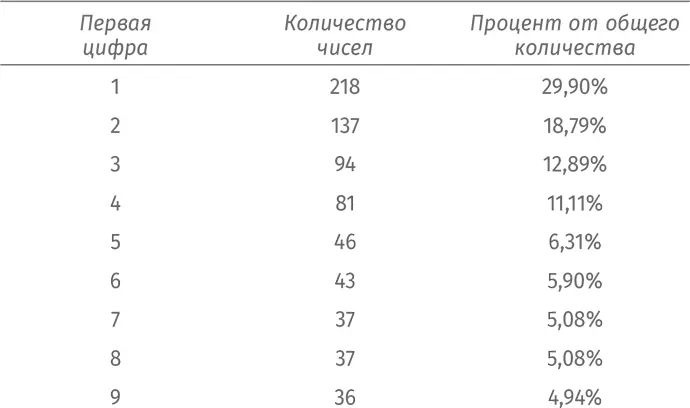
Нет резона останавливаться на перемножении трех чисел. Мы можем составить четырехмерные, пятимерные, шестимерные таблицы умножения и т. д. Давайте сразу посмотрим, что получится с десятимерной таблицей умножения [114] В десятимерной таблице умножения 9 10 произведений, то есть чуть меньше 3,5 миллиарда чисел. . Она содержит все возможные комбинации произведений десяти чисел от 1 до 9. Другими словами, мы проделываем следующие вычисления:

Занесем в таблицу, как много чисел начинается с 1, 2 и т. д.:

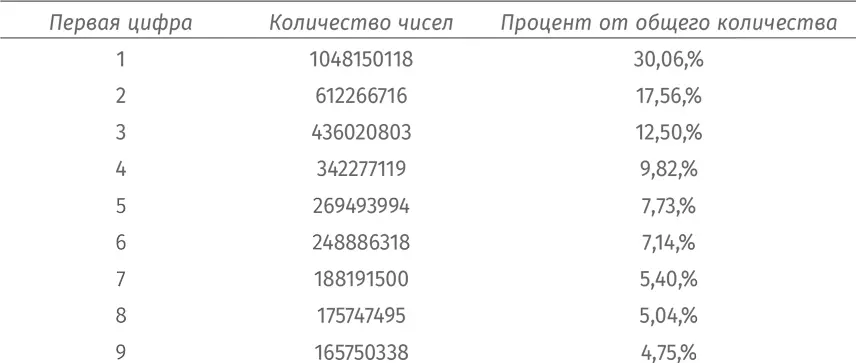
Мы увидим, что частотность первых цифр в этом случае уже хорошо согласуется с законом Бенфорда.

Перед тем как вникнуть в детали закона Бенфорда, давайте обратим внимание на одно его практическое применение.

Предположим, некий нечистый на руку человек подделывает налоговые декларации (меняет суммы, фабрикует баланс и т. д.). Короче говоря, он лжет и выдумывает числа, не имеющие отношения к реальности. Начальные цифры он выбирает случайным образом.

Судебный эксперт может быстро проверить, совпадает ли распределение первых цифр с законом Бенфорда. Если не совпадает, возникают подозрения, что числа подделаны. Но это еще не строгое доказательство вины.

Сверхбольшие и сверхмалые числа удобно записывать в экспоненциальном виде. Например, число 12 300 000 в экспоненциальном представлении выглядит так: 1,23 × 10⁷. Мы записываем число от 1 до 10, умноженное на степень 10. Основное число называется мантисса [115] От лат. mantissa – «прибавка». – Прим. пер. . Например, мантисса 853 100 000 равна 8,531:

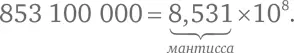
По определению, мантисса не может быть меньше одного и не может быть больше или равна десяти [116] Например, мантисса числа 0,0043 равна 4,3, потому что 0,0043 = 4,3 × 10 –3 . : 1 ≤ мантисса < 10.

Мантисса поможет нам сформулировать усовершенствованный вариант закона Бенфорда. Грубо говоря, закон гласит, что среди большого количества измерений около 30 % чисел имеют первую значащую цифру 1, то есть имеют мантиссу меньше 2.

Уточняя закон Бенфорда, мы можем присмотреться к первым двум цифрам большого количества измерений и задаться вопросом: с какой частотой мантисса будет, скажем, меньше 1,7? Вот другая формулировка того же вопроса: с какой частотой первые две цифры будут 10, 11, 12, 13, 14, 15 и 16?

В более общем виде: для любого числа m между 1 и 10 мы обозначим f ( m ) долю чисел, чья мантисса меньше m .

Например, f (2) – доля чисел, начинающихся на цифру 1. Величина f (3) означает долю чисел с начальной цифрой 1 и 2. Такая запись поможет понять, как возрастают частоты в законе Бенфорда.

Как использовать такую форму записи для обозначения доли измерений с начальной цифрой, скажем, 4?

• Заметим, что запись f (4) не означает, что начальная цифра равна 4. Это может быть также 1, 2 или 3.

• Точно так же запись f (5) означает, что первые цифры могут быть 1, 2, 3, 4.

• Чтобы выяснить, сколько чисел начинается на цифру 4, вычтем одну величину из другой: f (5) – f (4). Тогда мы исключим числа с начальной цифрой 1, 2, 3.

Есть две особые величины: чему равно f (1) и f (10)? Подумайте минуту, прежде чем читать дальше.

Вспомним: f ( m ) обозначает долю чисел с мантиссой меньше m . В то же время 1 ≤ m < 10. Что из этого следует?

• Нет ни одного числа с мантиссой меньше 1. Таким образом, f (1) = 0.

• Мантиссы всех чисел меньше 10. Таким образом, f (10) = 1 (или, если вам угодно, 100 %).

Между этими границами величина f ( m ) возрастает. Чем больше чисел с мантиссой меньше m , тем больше f ( m ).

Следующий шаг – понять, как f ( m ) зависит от m . Но вначале мы рассмотрим общий случай перехода из одной единицы измерения в другую.

Мы собрали тысячи измерений длин в километрах и увидели закон распределения первых цифр. Если мы переведем километры в мили, распределение не изменится. Измерения внутреннего валового продукта в долларах США дают примерно такую же частотность первых цифр. Ничего не изменится, если мы будем измерять ВВП в евро (или британских фунтах, или российских рублях). Но давайте присмотримся к переводу ярдов в футы.