Эдвард Шейнерман - Путеводитель для влюбленных в математику

20! = 2 432 902 008 176 640 000.

По формуле (C):

20! = 2 422 786 846 761 133 393,6839075390.

Погрешность равна около 0,4 %. Если мы перепрыгнем к N = 1000, погрешность составит менее 0,01 %.

Число 145 называют факторионом , потому что оно обладает волшебным свойством. Если мы сложим факториалы составляющих его цифр, то получим то же самое число:

1! + 4! + 5! = 1 + 24 + 120 = 145.

Числа 1 и 2 тоже являются факторионами (но не ноль, как мы увидим чуть позже). Существует всего четыре факториона. Попробуйте самостоятельно найти четвертый.

Это сложновато без компьютерной программы. Ответ приведен в конце главы.

Многие испытывают необоримое желание ответить: «0! равен нулю!» (Второй восклицательный знак всего лишь подчеркивает экспрессивность этой фразы.) Первый множитель в N ! равен N , а умножение на ноль дает ноль. Однако математики договорились, что 0! = 1, и я завершу главу разъяснением этого факта.

В главе 1 мы обсудили концепцию пустого произведения – умножения при отсутствии элементов. Факториал нуля – пример пустого произведения. Для любого N факториал представляет собой результат перемножения N элементов. Это ясно для положительных значений N , но это верно и для N = 0. По определению, при подсчете N ! мы перемножаем все целые числа от 1 до N . В случае N = 0 таких чисел просто-напросто нет, и произведение оказывается пустым. По договоренности, пустое произведение равно 1.

А вот еще одно обоснование того, почему 0! = 1. При подстановке N = 1 в формулу (B) мы получаем:

N ! = N × ( N – 1)! => 1! = 1 × 0!

Поскольку 1! = 1, мы получаем 0! = 1.

А теперь давайте вернемся к расстановке книг на полке. Сколькими способами можно расставить на полке ноль книг? Есть один-единственный вариант: оставить полку пустой.

Для нас очевидно, что все цифры сотворены равными. Нет, мы не имеем в виду «равными друг другу» – разумеется, нет! Но внутри нас теплится вера в то, что все десять цифр, от 0 до 9, играют одинаковые роли в мире чисел.

Печальная правда заключается в том, что числа могут быть такими же нескромными, как люди: они все стремятся к первенству. Представьте, что вам приглянулась вещь стоимостью 43,52 доллара. Какая из цифр кажется вам более значимой? Важнее всего для вас цифра четыре, а двойка на конце не играет почти никакой роли. Вы встревожитесь, если четверка вдруг изменится на девятку, а если изменится двойка, вряд ли вас это сильно взволнует.

Тот, кто ждет от Вселенной справедливости, должен верить, что у всех цифр одинаковые шансы сыграть значимую роль, – но бедный, бедный нолик! Он не становится первой значащей цифрой, честь выпала на долю других [105] Скажем, в числе 0,053 первая значащая цифра 5. Когда мы говорим о первой значащей цифре, то подразумеваем первую цифру, отличную от нуля. . Все они стремятся быть значительней остальных настолько часто, насколько это возможно.

Мы верим, что цифры от 1 до 9 участвуют в математике на равных правах и каждая начинает одну девятую часть всех существующих чисел (примерно 11 %). Разумеется, не может быть большего количества чисел, начинающихся с двойки, чем с пятерки.

Ведь так?

Утверждение о том, что все цифры от 1 до 9 равно представлены в качестве первой значащей цифры, приобретает смысл, если иметь в виду определенный диапазон чисел: скажем, от 1 до 999 999. В этом случае все цифры от 1 до 9 одинаково часто занимают место первой значащей цифры.

Разумеется, на результат влияет, какой именно диапазон мы выбрали. Если мы посмотрим на другой ряд чисел, скажем от 1 до 19, то обнаружим, что здесь все цифры от 2 до 9 занимают первую позицию всего единожды, в то время как 1 становится первой значащей цифрой в 11 случаях.

Ради беспристрастности давайте возьмем какие-нибудь величины из внешнего мира. Мы должны быть аккуратными и не искать числа, сконцентрированные в узком диапазоне. Поэтому мы не станем брать такой параметр, как рост взрослого человека [106] Если измерять рост в футах, почти все результаты будут начинаться с цифр 4, 5 или 6. , ведь практически все результаты измерений будут начинаться с 1 или 2 (ничтожно малое количество людей имеет рост выше 299 или ниже 100 сантиметров).

Ради уверенности в том, что все цифры имеют одинаковые шансы стать первой значащей цифрой числа, мы будем вести измерения в широком диапазоне. Например, давайте зададимся вопросом, насколько велико население разных стран [107] Я черпаю данные из «Справочника ЦРУ по странам мира». Он доступен в Сети по адресу https://www.cia.gov/library/publications/the-world-factbook . . Это значение будет колебаться от миллиарда с лишним (Китай и Индия) до менее чем десяти тысяч (в случае с карликовым государством на коралловом острове Науру [108] Согласно актуальной версии справочника ЦРУ, в Китайской Народной Республике 1 379 302 771 граждан, в Республике Индия 1 281 935 911, в Республике Науру 9642 (все данные проверены в июле 2017). Наименьшее в мире количество граждан у Ватикана: 1000 человек (проверено в 2017 году). – Прим. пер. ). Вдобавок к численности населения давайте выясним следующие параметры для сотен государств:

– валовой внутренний продукт (в долларах США);

– количество аэропортов;

– площадь (в квадратных километрах);

– ежегодную выработку электроэнергии (в киловатт-часах);

– ежегодное потребление продуктов нефтепереработки (в баррелях);

– общую длину всех железных дорог (в километрах);

– количество телефонов.

Таким образом, мы соберем около 2000 параметров и затем подсчитаем, сколько чисел начинается с цифры 1, сколько – с цифры 2 и т. д. Вот что у нас получится:

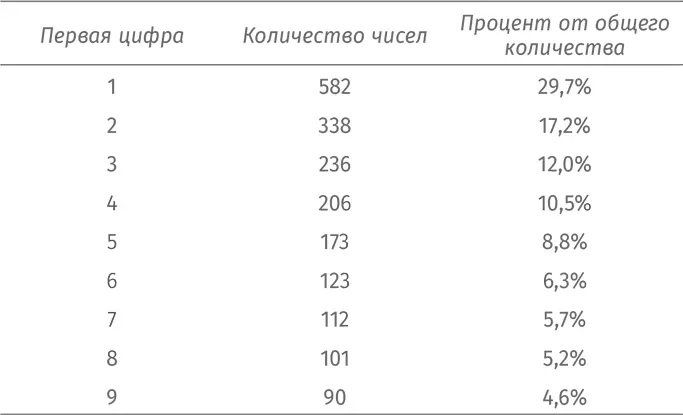
Невероятно: чаще всего на первой позиции встречается цифра 1 (примерно в 30 % случаев) и реже всего – цифра 9 (меньше 5 % случаев)!

Мы призываем читателей повторить эксперимент самостоятельно: взять статистический справочник, выписать первые цифры длин рек, высот гор, курсов акций, среднего роста различных видов животных, количества слов в романах, производства риса в разных странах и т. д.

Соберите как можно больше параметров, покрывающих широкий диапазон значений, и вы увидите все ту же логику. Чаще всего первой цифрой оказывается единица, реже всего – девятка.

Такое неравномерное распределение первых значащих цифр известно как закон Бенфорда , названный в честь Фрэнка Бенфорда [109] Фрэнк Бенфорд (1883–1948) – американский инженер и физик, бо́льшую часть жизни работал в General Electric. – Прим. пер. . Он опубликовал статью об этом феномене в 1938 году, хотя необходимо отметить, что еще в 1881 году к такому же выводу пришел Саймон Ньюком [110] Саймон Ньюком (1835–1909) – американский астроном, математик и экономист. Работал в Морской академии в Вашингтоне и Военно-морской обсерватории США. Двоюродный прапрадед физика Уильяма Ньюкома (о парадоксе, названном его именем, пойдет речь в главе 23). – Прим. пер. .