Эдвард Шейнерман - Путеводитель для влюбленных в математику

Предположим, мы измеряем огромное количество расстояний в ярдах и в футах и изучаем распределение первых цифр. Как много величин имеют первую значащую цифру 2? Это множество включает и 2,1, и 28, и 0,213, и 299,8 ярда. В обозначениях, которые мы приняли в предыдущем разделе, доля величин такого рода по отношению ко всем измерениям [118] Помните, что f (3) равно доле величин, мантисса которых меньше 3, а именно 1 или 2. Поэтому мы вычитаем долю измерений, начинающихся на 1. равна f (3) – f (2).

А теперь переведем наши измерения в футы. Иными словами, просто умножим всё на 3. 2,1 ярда равны 6,3 фута. Измерения в ярдах с первой значащей цифрой 2 превратятся в измерения с первой значащей цифрой от 6 до 9, не включая 9. Вы удивлены?

Вначале может показаться, что, если первая значащая цифра величин в ярдах равна 2, первая значащая цифра величин в футах будет равна 6. Это не так: 2,8 ярда равны 8,4 фута. Если мантисса измерений в ярдах находится в пределах от 2 до 3 (не включая 3), мантисса тех же измерений в футах будет в пределах от 6 до 9 (не включая 9).

Какая доля измерений имеет первую значащую цифру 6, 7 или 8? Ответ [119] Величина f (9) равна доле величин, мантисса которых меньше 9. Поэтому мы вычитаем долю величин, начинающихся на 1, 2, 3, 4 и 5. : f (9) – f (6).

Близится кульминация: мы имеем дело с одними и теми же измерениями в разных единицах длины, поэтому доля измерений в ярдах с мантиссой 2 будет равна доле измерений в футах с мантиссой 6, 7 или 8. Иными словами, f (3) – f (2) в ярдах равно f (9) – f (6) в футах. Посмотрите на рисунок. Оба прямоугольника символизируют всю совокупность наших измерений: первый прямоугольник – в ярдах, второй прямоугольник – в футах. Серая область в первом прямоугольнике обозначает измерения с мантиссой 2. Соответствующая область во втором прямоугольнике обозначает измерения с мантиссой 6, 7 или 8.

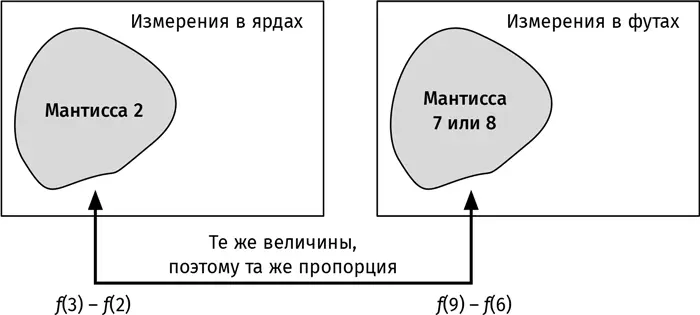
Важно понимать, что обе закрашенные области идентичны! Так что доля измерений в ярдах с мантиссой 2 равна доле измерений в футах с мантиссой 6, 7 или 8.

Рассмотрим более общий случай. Вообразим, что мы собрали множество измерений и хотим выяснить, сколько из них имеют мантиссу меньше определенного числа a . Доля величин, удовлетворяющих этому условию, равна f ( a ).

Мы переводим результаты в другие единицы измерения. Пусть коэффициент будет равен числу b [120] Если мы переведем ярды в футы, то b = 3. Для других величин это число другое. . Иными словами, если длина объекта в одних единицах измерения равна 23,5, в других она будет равна 23,5 × b .

Напомню, что f ( a ) равно доле величин с мантиссой от 1 до a , не включая a . Те же величины в других единицах имеют мантиссу строго меньше ab [121] Нас ждет прокол, если ab >10 или ab < 1. Эта проблема поддается разрешению, но пока мы просто будем рассматривать только варианты, при которых 1 ≤ ab ≤ 10. . Их доля равна f ( ab ).

На языке формул тезис о равенстве долей величин с мантиссой меньше a в одних единицах и с мантиссой меньше ab в других единицах выглядит так:

f ( a ) = f ( ab ) – f ( b ).

Или:

f ( ab ) = f ( a ) + f ( b ). (*)

Новый вопрос: какого рода функция удовлетворяет этому правилу и условиям f (1) = 0 и f (10) = 1?

Некоторые математические операции можно проделать наоборот. Например, мы возводим в квадрат какое-нибудь число: 6² = 36. А теперь проделываем обратную операцию – извлекаем квадратный корень: 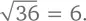Для положительных чисел операции возведения в квадрат и извлечения квадратного корня обратны друг другу. Операция, обратная возведению в степень, называется извлечением логарифма .

Например, 10⁴ = 10 000. Мы проделываем наоборот операцию возведения в степень и применяем логарифмическую функцию [123] В оригинале десятичный логарифм обозначен log в соответствии с американской традицией пропускать нижний индекс «10», когда речь идет о десятичном логарифме. В русскоязычной литературе используется обозначение lg( x ). – Прим. пер. :

lg(10 000) = 4.

Можно воспринимать логарифмическую функцию как ответ на вопрос: «В какую степень возводить?» В какую степень нужно возвести 10, чтобы получить некое число? Скажем, какая степень 10 дает 1000? Поскольку 1000 = 10 × 10 × 10 = 10³, ответ равен 3. Иными словами, lg(1000) = 3.

Несложно уяснить, что происходит, когда мы возводим 10 в степень, равную целому положительному числу, – мы просто перемножаем 10 заданное число раз:

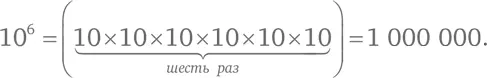
Если мы посчитаем нули в одной из степеней 10, то поймем значение логарифма:

lg(1 000 000 000) = 9.

Возведение 10 в дробную степень несколько сложнее. Ключевая идея здесь – понять, чему равно произведение 10 m и 10 ⁿ .

Чему равно произведение 10⁶ × 10⁵? Не бойтесь, перемножать десятки просто. Давайте распишем нашу формулу:

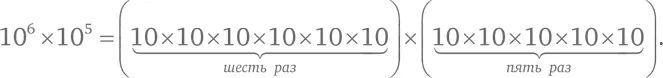
Каков результат? Нет нужды перемножать! Просто посчитайте, сколько раз встречается 10 в правой части формулы: одиннадцать. Иными словами,

10⁶ × 10⁵ = 10 11.

Таким образом, для целых положительных степеней

10 m × 10 ⁿ = 10 m + ⁿ .

Это тождество называется законом умножения степеней .

Ключевая идея вычисления дробной степени – применение данного закона для любых показателей степени. Давайте посмотрим, к чему это приведет.

Возьмем 10 0,5. Мы можем не знать, чему оно равно, но нам известно, чему равно произведение 10 0,5× 10 0,5. А именно:

10 0,5× 10 0,5= 10 0,5 + 0,5= 10.

Если умножить 10 0,5само на себя, получится 10. Таким образом, 10 0,5равно квадратному корню из десяти [124] Возьмите калькулятор, посчитайте обе величины и убедитесь, что я не ошибся. :

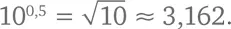
Так мы можем посчитать все степени 10. На рисунке вы видите график функции 10 х при x от 0 до 1.

При каком значении x выполняется условие 10 х = 2? При взгляде на график функции 10 х кажется, что подойдет x = 0,3. Если мы возьмем калькулятор, то выясним: 10 0,3≈ 1,99526… Близко, но не равно точно 2. Чуть-чуть увеличим степень. Попробуем x = 0,301; результат 10 0,301≈ 1,99986… Ближе, но все еще мимо цели. Нам нужно число немного больше. Величина x должна быть равна 0,30102999566398114… Это и будет log(2). (Вы уже встречали такое число раньше. Отыщите его!)