Эдвард Шейнерман - Путеводитель для влюбленных в математику

Я кладу свою находку во вторую стопку и повторяю процедуру с 99 неотсортированными тетрадями. Я сравниваю верхнюю тетрадь с 98 оставшимися. Поиск второй по алфавиту тетради потребует максимум 99 × 98 = 9702 сопоставления.

Третья тетрадь потребует максимум 98 × 97 сравнений, четвертая – максимум 97 × 96. Не исключено, что придется проделать 100 × 99 + 99 × 98 + 98 × 97 + … + 2 × 1 = 333 300 сравнений.

Мы проанализировали худший случай [127] Если мы вычислим среднестатистическое количество операций, то получим средний случай. . На каждой итерации мы нашли максимум из возможного числа операций и посчитали, сколько их всего потребуется. Несомненно, такой результат настраивает нас на пессимистический лад и показывает, насколько неэффективным был наш алгоритм. Давайте попробуем что-нибудь другое.

Мы снова начинаем со стопки из 100 тетрадей, перемешанных случайным образом. Берем первые две тетради. Если они идут не в правильном порядке, меняем их местами (первая станет второй, вторая – первой). Если порядок верный, оставляем все без изменений. Дальше смотрим на вторую и третью тетрадь. Если порядок верный, идем дальше. Если нет, меняем их местами. Так мы действуем по этому алгоритму, пока не доберемся до конца стопки. Один заход требует 99 сравнений.

Когда мы дойдем до конца стопки, тетради с именами из начала алфавита сместятся вверх, а тетради с именами в конце алфавита сместятся вниз. Но одного захода может быть недостаточно. В худшем случае первая по алфавиту тетрадь изначально лежала в самом низу, и в первом заходе мы переместили ее всего-навсего на 99-ю позицию. В этом случае сортировка потребует 99 операций [128] Описанную процедуру называют сортировкой пузырьковым методом . Диаграмма иллюстрирует один раунд алгоритма. Обратите внимание: тетрадь A сместилась всего на одну позицию. Нам потребуется еще шесть раундов, чтобы она поднялась наверх. .

Таким образом, нам придется проделать максимум 99 × 99 = 9801 операцию. Это гораздо лучше первого метода, но все еще неэффективно. Если сравнение и смена позиции требует двух секунд, я закончу спустя пять часов. Это никуда не годится.

И вот я в расстроенных чувствах выхожу из кабинета, чтобы развеяться. В коридоре я встречаю двух постдоков, которые работают под моим научным руководством. Зловещая улыбка змеится на моих губах. Я спешу обратно в кабинет, делю стопку неотсортированных тетрадей пополам и даю по 50 тетрадей каждому постдоку. «Вот вам стопка тетрадей, – говорю я. – Пожалуйста, рассортируйте их по алфавиту и принесите ко мне в кабинет, когда закончите». После чего с воодушевлением возвращаюсь к основной работе [129] Описанный метод называют сортировкой слиянием . Это хороший пример принципа «разделяй и властвуй»: сложная задача разбивается на несколько задач попроще, а затем решения объединяются. .

Мне предстоит доделать сортировку, когда постдоки выполнят задание. Нужно превратить две упорядоченные стопки в одну. Насколько это будет трудно? Допустим, у меня есть две стопки тетрадей в алфавитном порядке. Я смотрю на верхние тетради в той и другой стопке, выбираю первую по алфавиту и кладу в итоговую стопку. Диаграмма иллюстрирует процесс.

Когда одна из стопок иссякает, я просто-напросто кладу оставшуюся в конец итоговой стопки. В худшем случае придется проделать 99 операций. Это потребует всего несколько минут!

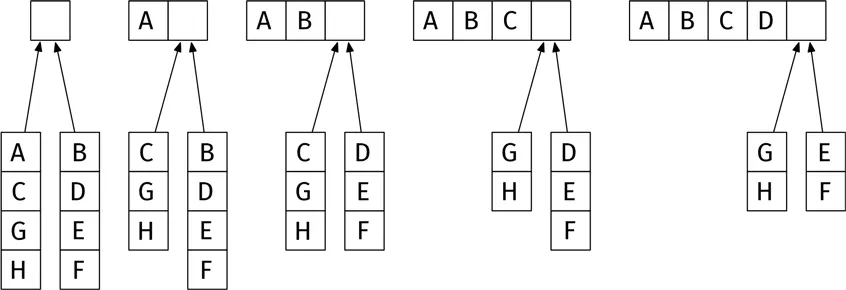
Но как насчет моих постдоков? У каждого стопка с 50 тетрадями. Постдоки – люди смышленые, поэтому не станут сортировать тетради самостоятельно. Они, в свою очередь, поделят свои стопки пополам (таким образом, в каждой окажется по 25 тетрадей) и передоверят сортировку аспирантам! Когда те закончат, постдокам останется соединить две отсортированные стопки по 25 тетрадей в одну общую по 50. Это потребует максимум 49 операций.

Но четыре аспиранта тоже не дураки. Они делят свои стопки на две части (в одной 12, в другой 13 тетрадей) и находят восемь старшекурсников, чтобы передоверить работу. В результате каждому аспиранту остается соединить две маленькие стопки и отдать их постдокам.

Как старшекурсники сортируют тетради? Несложно догадаться: они делят свои стопки на две части (в одной 6 тетрадей, в другой 7), ловят 16 третьекурсников и отдают им эти стопки. Те находят 32 второкурсника и отдают им раздербаненные стопки (в одних по 3, в других по 4 тетради). Наконец, второкурсники отлавливают 64 первокурсника и отдают им стопки по 1 и по 2 тетради. Первокурсникам делать нечего: они быстро сортируют свою часть и отдают обратно.

Очевидно, эта «схема Понци [130] Чарльз Понци – итальянский мошенник, создатель финансовой пирамиды в Бостоне в 1920 году. – Прим. пер. » экономит мое время, но насколько она эффективна в целом? Посмотрим, как много операций она потребует в худшем случае. Занесем все данные в таблицу:

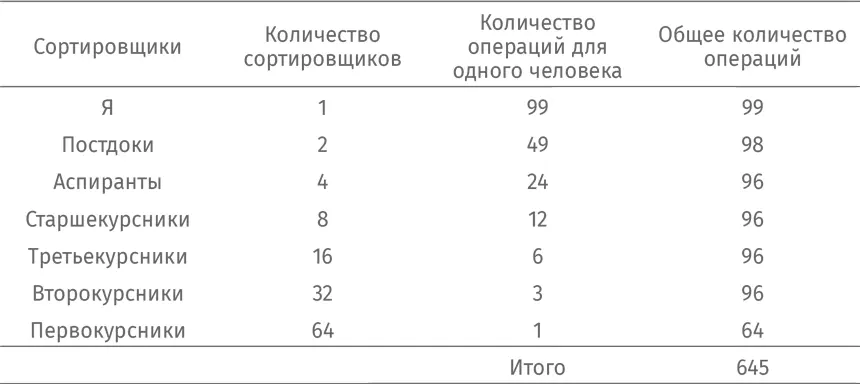
Максимальное количество операций оказывается существенно меньше, чем при сортировке пузырьковым методом.

К несчастью, в этой схеме есть изъян: у меня сейчас нет постдоков! Так что вместо вербовки целой армии помощников придется работать самому.

Для начала я найду большой незагроможденный стол. Я поделю стопку из 100 тетрадей пополам и положу две стопки по краям стола. Как я их отсортирую? По тому же алгоритму! Поделю две стопки по 50 тетрадей на четыре по 25, а их буду сортировать тем же методом. В худшем случае понадобится 645 операций. Правда, на сей раз мне придется действовать в одиночку. Однако это лучше, чем почти что 10 000 операций при сортировке пузырьковым методом.

Словарное определение не должно включать определяемого слова. Вообразите, что вы ищете в словаре слово оскудение и находите такое определение:

Оскудение: результат оскудения [131] Заметим, что пример не так прост, как кажется: первый раз слово «оскудение» обозначает состояние, а второй раз – процесс. – Прим. науч. ред. .

Что за чушь! Однако наш алгоритм сортировки и слияния грешит именно этой ссылкой на самого себя. Вот более точное определение.

На входе:объекты a 1, a 2, a 3, …, a n .

На выходе:те же объекты в отсортированном виде.

1. Если n = 1, сортировка закончена. Пускаем данные на выход. В противном случае переходим к пункту 2.

2. Поделить множество объектов на равные подмножества, если их количество четно, или на подмножества, отличающиеся на единицу, если количество нечетно. Использовать алгоритм сортировки и слияния.