Эдвард Шейнерман - Путеводитель для влюбленных в математику
- Название:Путеводитель для влюбленных в математику
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2018
- Город:Москва
- ISBN:978-5-9167-1131-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Эдвард Шейнерман - Путеводитель для влюбленных в математику краткое содержание
Путеводитель для влюбленных в математику - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
b = ue, c = ve ,
где u и v – целые числа. Следовательно,
a = c + qb = ve + q ( ue ) = ( v + qu ) e ,
и e – еще и делитель a .
Итак, мы доказали, что общие делители a и b совпадают с общими делителями b и c . Таким образом,
НОД ( a, b ) = НОД ( b, c ). (C)
Посмотрим, как тождество (C) позволит нам эффективно вычислить наибольший общий делитель двух больших целых чисел: a = 10 693 и b = 2220.
Мы делим a на b и видим, что 2220 умещается в 10 693 четыре раза [136] 10 693 = 4 × 2220 + 1813.
, при этом остаток c = 1813. Следовательно,
НОД (10 693, 2220) = НОД (2220, 1813).
Переходим к следующей итерации. Введем обозначения a ' = 2220 и b ' = 1813. Поделим a ' на b ' и увидим, что 1813 умещается в 2220 всего один раз [137] 2220 = 1 × 1813 + 407.
и остаток c ' = 407. На основании тождества (C)
НОД (10 693, 2220) = НОД (2220, 1813) = НОД (1813, 407).
На новом шаге a '' = 1813 и b '' = 407. После деления мы обнаружим, что 407 умещается внутри 1817 четыре раза [138] 1813 = 4 × 407 + 185.
и остаток c '' = 185. Опять-таки на основании (C)
НОД (10 693, 2220) = НОД (2220, 1813) = НОД (1813, 407) = НОД (407, 185).
На сей раз мы имеем дело с числами a ''' = 407 и b ''' = 185. Деление показывает, что 185 умещается внутри 407 два раза [139] 407 = 2 × 185 + 37.
и остаток равен c ''' = 37. Таким образом,
НОД (10 693, 2220) = НОД (2220, 1813) = НОД (1813, 407) = НОД (407, 185) = НОД (185, 37).
Мы почти у цели! Делим a '''' = 185 на b '''' = 37 и – подумать только! – получаем ровно 5. Следовательно, НОД (185, 37) = 37. Завершаем наши выкладки:
НОД (10 693, 2220) = НОД (2220, 1813) = НОД (1813, 407) = НОД (407, 185) = НОД (185, 37) = 37.
Мы нашли наибольший общий делитель 10693 и 2220, проделав всего пять операций деления!
Алгоритм Евклида для поиска наибольшего общего делителя [140] В главе 6 мы познакомились с концепцией взаимно простых чисел. Вот альтернативное определение: число a взаимно простое с b , если НОД ( a, b ) = 1. Так как алгоритм Евклида позволяет эффективно вычислить НОД двух чисел, он также позволяет выяснить, являются ли два числа взаимно простыми.
можно сформулировать так:
На входе:два положительных целых числа a и b .
На выходе:НОД ( a, b ).
1. Найти частное q и остаток c при делении a на b .
2. Если c = 0, то НОД ( a, b ) = b .
3. В противном случае вычислить НОД ( b, c ) = НОД ( a, b ).
Проверьте, насколько хорошо вы усвоили алгоритм Евклида, и вычислите НОД (1309, 1105). Можете воспользоваться калькулятором. Сверьтесь с ответом в конце главы.
Концепция наибольшего общего делителя тесно связана с концепцией наименьшего общего кратного . Для двух положительных целых чисел (допустим, 10 и 15) наименьшее общее кратное – это самое маленькое положительное целое число, которое делится на то и на другое; в нашем случае ответ равен 30. Мы будем использовать обозначение НОК ( a, b ).
Наименьшее общее кратное полезно при сложении дробей. Например, для сложения 1/10 и 1/15 вначале нужно привести обе дроби к общему знаменателю. Это может быть любое число, которое делится на 10 и на 15; проще всего найти НОК. Так как НОК (10, 15) = 30, то
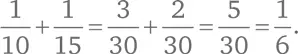
Найти наименьшее общее кратное для маленьких чисел не слишком сложно, но как быть с большими числами? Скажем, чему равно наименьшее общее кратное 364 и 286?
Один вариант состоит в том, чтобы последовательно выписывать числа, кратные первому и второму, и уповать, что рано или поздно они совпадут [141] Данный метод неэффективен, однако не безнадежен. Мы знаем, что 364 × 286 кратно тому и другому числу. Будем надеяться на то, что набредем на общее кратное поменьше.
:
числа, кратные 364 → 364, 728, 1092, 1456, 1820, 2184, …
числа, кратные 286 → 286, 572, 858, 1144, 1430, 1716, 2002, …
Вскоре мы дойдем до 4004 и запишем ответ: НОК (364, 286) = 4004.
Вот еще одна идея. Разложим 364 и 286 на простые множители:
364 = 2 × 2 × 7 × 13;
286 = 2 × 11 × 13.
Числа, кратные 364, должны делиться на 2 × 2 × 7 × 13, а числа, кратные 286, должны делиться на 2 × 11 × 13. При конструировании наименьшего общего кратного мы должны воспользоваться этими простыми числами – два раза по 2, затем 7, 11 и 13 (нам ни к чему брать два раза по 13):
2 × 2 × 7 × 11 × 13 = 4004.
Разумеется, 4004 и есть наименьшее общее кратное 364 и 286.
Этот метод выглядит потрясающе, однако – как я уже объяснил в главе 1 – мы не знаем эффективного алгоритма разложения больших чисел на простые множители.
Хотя разложение на простые множители не дает достаточно эффективного алгоритма вычисления НОК двух чисел, оно делает важную подсказку. Давайте сравним, как используется разложение на множители при вычислении НОК и НОД.
Вот семь простых множителей двух чисел, взятые вместе:
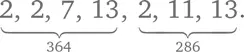
Мы находим НОД (364, 286) с помощью двух общих простых делителей: 2 и 13.
Для вычисления НОК (364, 286) нам нужны все простые числа в двух списках, хотя нет нужды брать два раза по 13 (достаточно одного) и три раза по 2 (достаточно двух). Иными словами, мы берем каждое простое число из того списка, где оно встретилось большее число раз. Таким образом, нам нужны пять чисел: 2, 2, 7, 11 и 13.
Проверяем:
НОД (364, 286) = 26 = 2 × 13;
НОК (364, 286) = 4004 = 2 × 2 × 7 × 11 × 13.
Заметим, что при подсчете НОК мы выкинули именно те числа, которые нужны для вычисления НОД:
Иначе говоря,
364 × 286 = (2 × 2 × 7 × 13) × (2 × 11 × 13) = (2 × 2 × 7 × 11 × 13) × (2 × 13) = НОК (364, 286) × НОД (364, 286).
Мы можем обобщить этот пример. Для любых двух целых положительных чисел a и b
a × b = НОК ( a, b ) × НОД ( a, b ).
Таким образом,
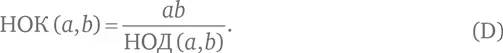
Так как алгоритм Евклида позволяет эффективно вычислить наибольший общий делитель двух чисел, он также годится – с учетом тождества (D) – для эффективного вычисления наименьшего общего кратного.
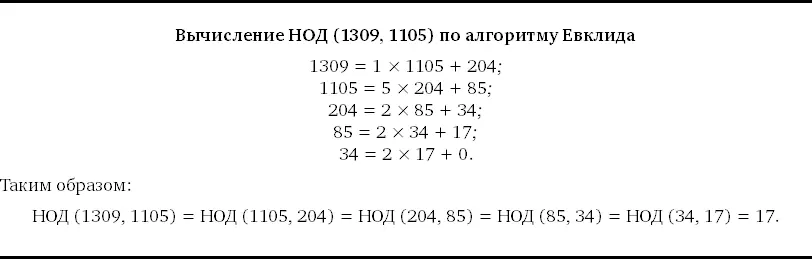
Часть II
Геометрические фигуры
Глава 13
Треугольники
Треугольник – геометрическая фигура, состоящая из трех прямых отрезков, соединяющих три точки. В главе 13 мы рассмотрим общеизвестные свойства этих незамысловатых фигур и приподнимем покров над их тайнами. А начнем мы с двух всем знакомых формул: суммы углов и площади треугольника.
Возможно, самый известный факт, касающийся треугольников, – то обстоятельство, что если мы измерим все три угла и сложим эти величины, то получим 180°.
Читать дальшеИнтервал:
Закладка:










