Эдвард Шейнерман - Путеводитель для влюбленных в математику

Теорема Пика [144] Георг Пик (1859–1942) – австрийский математик, профессор Университета Карла-Фердинанда в Праге. – Прим. пер. предлагает кое-что полегче. Мы не будем считать квадратики – мы посчитаем координатные точки. Вначале найдем, сколько точек внутри треугольника; обозначим их число I . Затем посчитаем количество точек на границе треугольника; обозначим их число B .

Теорема Пика утверждает:

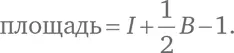
Я начертил достаточно крупный треугольник, чтобы вы смогли сосчитать все точки. В итоге получится, что I = 38, а B = 10 (включая вершины). Таким образом,

Завершу этот раздел небольшой головоломкой. Предположим, мы хотим найти площадь четырехугольника с целочисленными вершинами. Если внутри четырехугольника I координатных точек, а на границе B координатных точек (включая четыре вершины), то чему равна его площадь? Ответ вы найдете в конце главы.

Кроме того, подумайте над вопросом о площади других многоугольников с целочисленными вершинами: пятиугольнике, шестиугольнике и т. д.

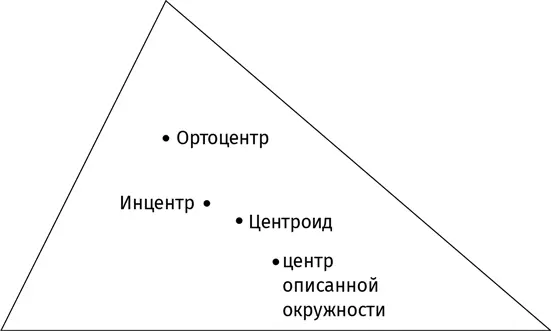
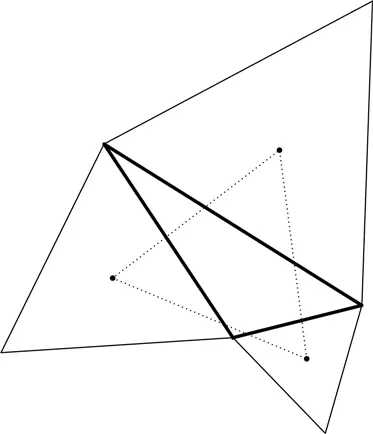
Что мы подразумеваем, когда говорим «центр треугольника»? У этого понятия есть несколько значений, и каждое интересно по-своему.

Начнем с точки под названием центроид треугольника. Соединим вершины треугольника с серединами противоположных сторон. Такие отрезки называют медианами . Удивительно: все три медианы пересекаются в одной точке; ее и называют центроидом.

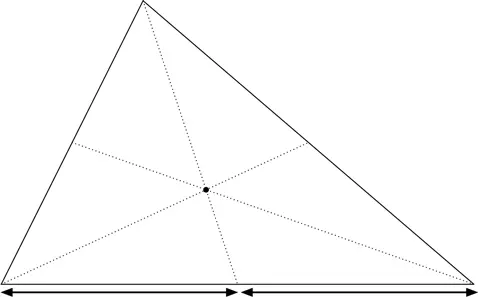
Одно из свойств центроида – он представляет собой центр масс треугольника: если треугольник из жесткого материала (скажем, из тонкого листа железа) подвесить за центр масс, он будет сохранять равновесие. Разумеется, равновесие окажется шатким, если наши вычисления окажутся недостаточно точными.

Мы уже провели отрезки из вершин треугольника к серединам противолежащих сторон; теперь давайте проведем кратчайшие линии, соединяющие вершины и противолежащие стороны. Они будут пересекать стороны треугольника под прямыми углами. Ко всеобщему восхищению эти три отрезка также пересекаются в одной точке; ее называют ортоцентр .

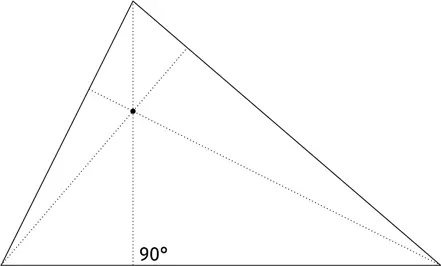
Далее: биссектрисы. Проведем три отрезка из трех вершин до трех противоположных сторон, чтобы каждый из них рассекал соответствующий угол треугольника на два равных между собой угла. Эти три отрезка вновь пересекаются в одной точке, известной как инцентр .

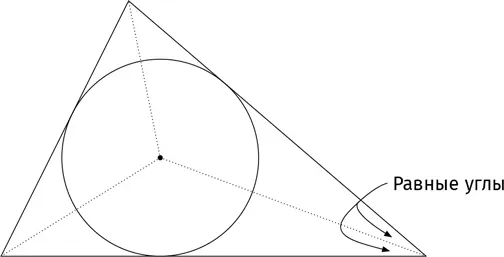
Инцентр называют так потому, что это центр окружности, касающейся всех трех сторон треугольника ( вписанной в треугольник окружности ).

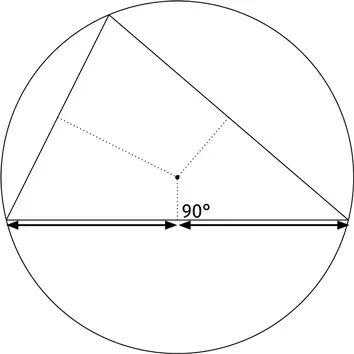
Теперь проведем отрезки не из вершин треугольника, а из середин его сторон, причем под прямыми углами к этим сторонам; их называют серединные перпендикуляры . Имею счастье сообщить, что и они пересекаются в одной точке – в центре окружности, описанной около треугольника , то есть содержащей все три его вершины.

Эти четыре центра (центроид, ортоцентр, инцентр и центр описанной окружности) совпадают, если треугольник равносторонний. Но в общем случае точки различаются. На рисунке вы можете видеть расположение всех четырех центров в некотором произвольном треугольнике [145] Как ни странно, некоторые из четырех центров могут лежать вне треугольника! Догадываетесь почему? Ответ – в конце главы. .

Вместо биссектрис проведем трисектрисы углов треугольника – отрезки, рассекающие каждый угол треугольника на три равные между собой части. В общей сложности это будет шесть отрезков (по два для каждого угла). Разумеется, все они не могут пересечься в одной точке, но точки, где они пересекаются, образуют малый треугольник внутри большого.

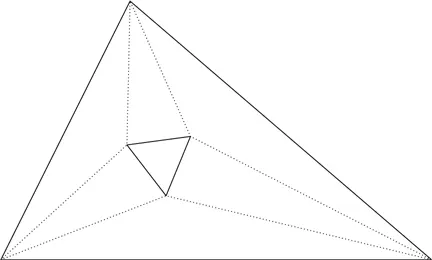
Ошеломительная теорема Морли [146] Фрэнк Морли (1860–1937) – заведующий кафедрой в Университете Джонса Хопкинса в Балтиморе, главный редактор American Journal of Mathematics. Он доказал эту теорему в 1899 году, когда изучал свойства кривых, заданных кубическим уравнением. – Прим. пер. утверждает, что этот малый треугольник всегда будет равносторонним!

Можно отыскать и другой равносторонний треугольник, сопутствующий любому произвольно взятому треугольнику. Построим на трех сторонах треугольника (на рисунке он начерчен жирными линиями) три равносторонних треугольника (начерчены тонкими линиями). Отметим центры этих равносторонних треугольников:

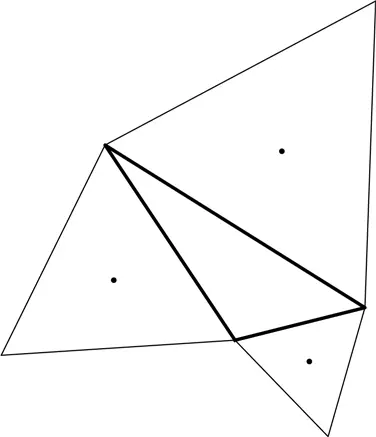
Соединим три центра и – вуаля! – получим очередной равносторонний треугольник.

Нарисуем четырехугольник с целочисленными вершинами на клетчатой бумаге и проведите диагональ. Таким образом, мы получаем два треугольника с общей стороной:

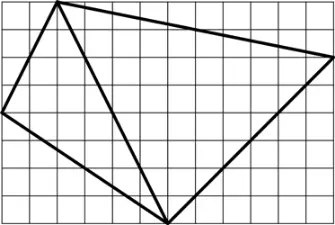
Мы можем посчитать площади двух треугольников, пользуясь теоремой Пика, а затем сложить получившиеся величины. Обозначим эти два треугольника L и R и получим:

Таким образом, площадь четырехугольника равна 16 + 36 = 52.

Но, ко всеобщему восхищению, теорема Пика верна также для четырехугольников! И вот почему.

Вместо нового пересчета точек давайте воспользуемся результатами, уже полученными ранее.

Внутри левого треугольника 13 точек, внутри правого – 31 точка. Обратите внимание, что три точки на диагонали тоже лежат внутри четырехугольника; включим их в наши расчеты. Это дает I Q = 31 + 13 + 3 = 47.