Эдвард Шейнерман - Путеводитель для влюбленных в математику

Вернемся к процедуре поиска пифагоровых троек. Начнем с комплексного числа z = x + yi , где x и y – целые числа [157] Комплексное число z = x + yi , где x и y – целые числа, называют гауссовым целым числом. . Абсолютная величина z может не быть целым числом, но оно представляет собой квадратный корень из целого числа: 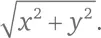Абсолютная величина z ² непременно будет целым числом: | z ²| = | z |² = x ² + y ². Найдем z ²:

z ² = ( x + yi ) × ( x + yi ) = ( x ² – y ²) + (2 xy ) i .

Пусть a = x ² – y ², b = 2 xy, c = x ² + y ². Тогда | a + bi | = c ; следовательно, a ² + b ² = c ².

Последний пример: пусть z = 7 + 4 i . Его квадрат равен 33 + 56 i , абсолютная величина этого числа равна

Еще одна пифагорова тройка: 33, 56, 65.

Я продемонстрировал процедуру поиска пифагоровых троек. Возникает естественный вопрос: все ли пифагоровы тройки можно найти подобным образом? Да, но доказательство этого факта довольно сложное, так что, если вам интересно, я рекомендую обратиться к литературе по теории чисел.

Мы рассмотрели тройки целых чисел, удовлетворяющих уравнению теоремы Пифагора. Они лишь косвенным образом связаны с миром прямоугольных треугольников. Сейчас мы полностью перенесемся за пределы геометрии и подумаем о решениях уравнения aⁿ + bⁿ = cⁿ .

Легко найти тройки целых чисел a, b, c , удовлетворяющих соотношению a + b = c . В предыдущем разделе я рассказал о способе поиска троек целых чисел, удовлетворяющих уравнению a ² + b ² = c ². Сейчас нам предстоит перейти к более высоким степеням: можем ли мы найти тройки целых чисел, удовлетворяющих уравнению a ³ + b ³ = c ³, или a ⁴ + b ⁴ = c ⁴, или a ⁵ + b ⁵ = c ⁵ и т. д.?

Вот два неинтересных решения уравнения a ³ + b ³ = c ³:

5³ + 0³ = 5³; 5³ +(–5)³ = 0³.

Куда сложнее найти тройки целых чисел, не равных нулю , которые являются решениями уравнения a ³ + b ³ = c ³. Такие решения называются нетривиальными .

Этот вопрос в 1637 году заинтересовал Пьера Ферма. На полях «Арифметики» Диофанта он сформулировал следующее утверждение: уравнение aⁿ + bⁿ = cⁿ не имеет нетривиальных целочисленных решений при n ≥ 3. Он записал по-латыни знаменитые слова:

Невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него [158] Эта история – священный миф математического сообщества, она пересказана во множестве книг и статей. Действительно ли Ферма нашел доказательство? Сомнительно. Более интересный вопрос: Ферма верил, что нашел доказательство, или разыгрывал читателей? Я предпочитаю второй вариант. .

Это утверждение известно как великая теорема Ферма , хотя сомнительно, что Ферма мог доказать ее. Потребовалось три столетия, прежде чем Эндрю Уайлс [159] Сэр Эндрю Джон Уайлс (род. 1953) – британский и американский математик, профессор Оксфордского университета. – Прим. пер. нашел доказательство и опубликовал его в середине 1990-х. Он показал, что теорема Ферма верна и уравнение aⁿ + bⁿ = cⁿ не имеет нетривиальных целочисленных решений при n ≥ 3.

Окружности изящны и красивы. Глава 15 содержит россыпь любопытных фактов об этих основополагающих геометрических фигурах.

Математики избегают туманных определений, им подавай точность! Окружность – это множество точек на плоскости, равноудаленных от некоторой точки [160] Математики различают окружность (линию) и круг (участок плоскости, ограниченный окружностью). (Точно так же различаются сфера (поверхность) и шар (область пространства, ограниченная сферой). – Прим. науч. ред. ) . Давайте распутаем этот клубок.

Прежде всего, окружность представляет собой множество точек. Естественно, не любое множество точек образует окружность. Речь идет лишь об избранных точках. Избранных по какому принципу? Окружность – это множество точек, заданных двумя условиями: положительным числом r и точкой X . Как вы знаете, точку X мы называем центром окружности, а число r – радиусом .

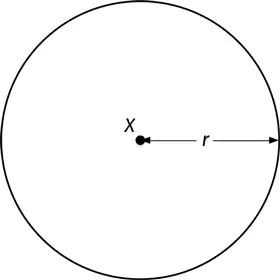
При построении (чернилами на бумаге или пикселями на экране) окружность имеет некоторую толщину, но с математической точки зрения толщина окружности равна нулю.

Окружности – близкие родственники сфер . А что такое сфера? Это множество точек в пространстве, равноудаленных от некоторой точки. Обратите внимание: два определения почти одинаковы, за исключением того, что окружность находится в плоскости.

Точки на плоскости задаются двумя координатами: x и y . Если мы записываем уравнение с двумя переменными, множество точек, чьи координаты удовлетворяют этому уравнению, задают какую-нибудь геометрическую фигуру.

Например, уравнению x ² + y ² = 1 удовлетворяют некоторые, но не все точки плоскости. Скажем, точка с координатами (1, 0) удовлетворяет уравнению, потому что 1² + 0² = 1. Точно так же точка (3/5, 4/5) тоже удовлетворяет уравнению:

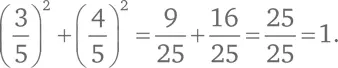
С другой стороны, точка (1/2, 1/2) не удовлетворяет уравнению, потому что

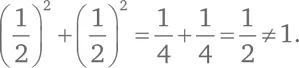
Что можно сказать о точках, удовлетворяющих уравнению x ² + y ² = 1? Они задают окружность с центром в начале координат и радиусом 1.

Почему? Давайте подумаем о точке ( x, y ). Она задает прямоугольный треугольник. Проведем перпендикуляры к осям абсцисс и ординат и соединим отрезком нашу точку с началом координат, как показано на рисунке.

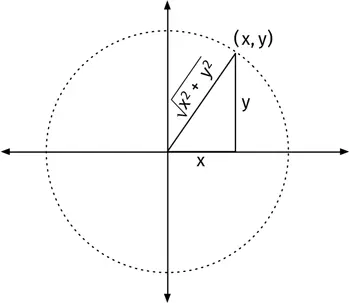
Длины катетов треугольника равны x и y , и по теореме Пифагора (см. главу 14) длина гипотенузы равна 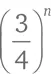Это не что иное, как расстояние от точки ( x, y ) до точки (0, 0).