Эдвард Шейнерман - Путеводитель для влюбленных в математику

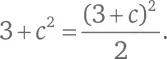
Решение квадратного уравнения дает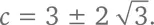

Таким образом,

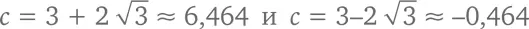
Отрицательное число нам не подходит, ведь как радиус/кривизна окружности может быть меньше нуля? Таким образом, кривизна малой окружности равна примерно 6,464, а радиус – примерно 0,1547.

Четыре окружности могут «поцеловаться» иначе. Начертим снова три окружности, касающиеся друг друга, но вместо малой окружности внутри опишем большую окружность, касающуюся всех трех окружностей снаружи:

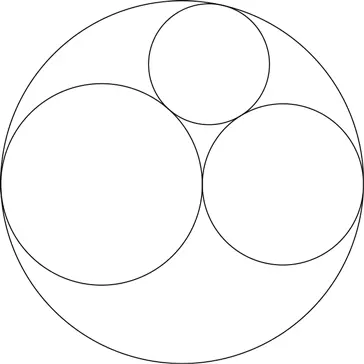
Хорошая новость: решение Декарта по-прежнему остается в силе. Фокус состоит в том, чтобы взять отрицательный корень квадратного уравнения с обратным знаком!

Например, давайте снова рассмотрим три окружности с радиусом 1. Формула (*) вновь приводит нас к двум ответам. Но теперь большая окружность имеет кривизну где-то 0,464 и радиус где-то 2,1547.

Иначе говоря, формула Декарта работает и в том случае, когда мы вычисляем радиус малой окружности внутри трех, касающихся друг друга, и в том случае, когда мы ищем радиус большой окружности, охватывающей эти три.

Если корень уравнения отрицательный, речь идет об описанной окружности; в случае положительного корня речь идет о вписанной окружности. А теперь другой вопрос: что означает нулевая кривизна ? Сама формулировка подсказывает, что «окружность» с нулевой кривизной представляет собой прямую линию [165] Соответственно, когда кривизна стремится к бесконечности, окружность схлопывается в точку. – Прим. пер. .

Решение Декарта в 1930-е годы заново открыл Фредерик Содди [166] Фредерик Содди (1877–1956) – английский радиохимик, лауреат Нобелевской премии 1921 года «за вклад в химию радиоактивных веществ и за исследование происхождения и природы изотопов». – Прим. пер. . Он был настолько поражен элегантностью формулы, что сочинил стихотворение под названием «Прицельный поцелуй». Вот вторая строфа, где зарифмована формула (*):

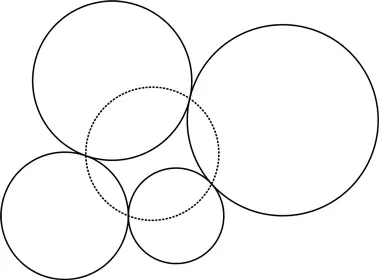
Есть еще один вариант поцелуя четырех окружностей. На сей раз они будут касаться друг друга попарно, выстроившись в кольцо. Иными словами, касаются первая и вторая окружности, вторая и третья, третья и четвертая, четвертая и первая. Итого мы имеем четыре точки соприкосновения.

Удивительно, но факт: эти четыре точки всегда будут лежать на другой окружности, пятой по счету.

Я завершу эту главу теоремой, доказанной Блезом Паскалем [167] Блез Паскаль (1623–1662) – французский математик, физик и философ. – Прим. пер. .

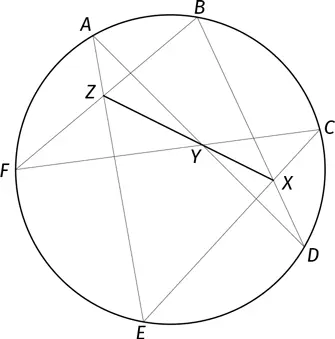
Расставим на окружности шесть точек: A, B, C, D, E и F . Соединим их отрезками, чтобы возник перекрученный шестиугольник:

A → D → B → F → C → E → A .

Теорема Паскаля говорит о том, что три точки, в которых пересекаются пары отрезков DB и CE, AD и FC, BF и EA (на чертеже они отмечены буквами X, Y, Z соответственно) всегда будут лежать на одной прямой!

Отмечу, что теорема Паскаля верна и в случае шести точек, лежащих на эллипсе [168] В общем виде теорема Паскаля формулируется так: если шестиугольник (выпуклый или самопересекающийся) вписан в окружность или любое другое коническое сечение (эллипс, параболу, гиперболу), точки пересечения трех пар противоположных сторон лежат на одной прямой. – Прим. пер. .

Предположим, все круги имеют радиус 1. Центры четырех соседних кругов расположены на вершинах ромба со стороной 2.

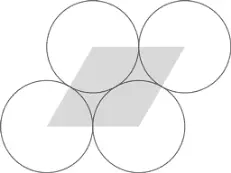
Ромб состоит из двух равносторонних треугольников. Высота равностороннего треугольника [169] Высота равностороннего треугольника со стороной 2 рассекает его на два прямоугольных треугольника с гипотенузой длиной 2 и катетом длиной 1. По теореме Пифагора мы можем вычислить длину оставшегося катета. со стороной 2 равна √3. Таким образом, площадь треугольников равна

Площадь ромба вдвое больше: 2√3

Теперь давайте подумаем, какой процент площадей кругов покрывает ромб. Два круга покрыты на 1/6 и еще два – на 1/3. Все вместе дает площадь одного круга с радиусом 1, то есть π.

Соотношение покрытой кругами площади к общей площади равно

Равносторонний треугольник – это геометрическая фигура, состоящая из трех равных между собой отрезков, пересекающихся под углом 60°. Квадрат – фигура, состоящая из четырех равных между собой отрезков, пересекающихся под углом 90°. Это примеры правильных многоугольников – фигур, состоящих из равных между собой прямых отрезков, пересекающихся под равными углами. На рисунке изображен правильный семиугольник (гептагон [170] Стороны правильного семиугольника имеют равную длину, и углы также равны между собой. Головоломка. Углы правильного семиугольника равны между собой. Но чему они равны? Подсказка: помните, что сумма углов треугольника равна 180°. Ответ – в конце главы. ).

Некоторые дорожные знаки (например, знак «Движение без остановки запрещено») имеют форму правильного восьмиугольника (октагона).