Эдвард Шейнерман - Путеводитель для влюбленных в математику

Во-первых, напомню формулу Эйлера:

V – E + F = 2. (A)

Во-вторых, мы будем использовать прием со штрихами, чтобы выяснить соотношение между E, V и r . Пометим штрихом оба конца каждого ребра. Общее количество штрихов – 2 E . Кроме того, мы нанесем r штрихов возле каждой вершины, обозначив сходящиеся там ребра; всего у нас будет rV штрихов. Если все проделать аккуратно, оба числа совпадут:

2E = rV . (B)

В-третьих, выясним соотношение между E, F и n . Нам снова поможет прием со штрихами, но на сей раз мы станем наносить их, постепенно двигаясь по граням . Будем поочередно помечать штрихом ребра каждой грани. Как и раньше, на каждом ребре окажется по два штриха (так как оно отделяет две грани). Итак, с одной стороны, количество штрихов 2 E, а с другой стороны, количество штрихов nF ( n штрихов на каждой из F граней). Таким образом,

2E = nF . (C)

Давайте убедимся, что формулы (A), (B) и (C) верны для додекаэдра:

V – E + F = 20–30 + 12 = 2;

2 E = 2 × 30 = 60 = 3 × 20 = rV ;

2 E = 2 × 30 = 60 = 5 × 12 = nF .

Сделаем еще кое-что.

Исходя из (B), мы имеем 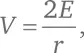а исходя из (C), мы получаем 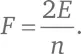Подставим эти значения в формулу (A):

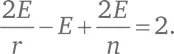
Поделим на 2 E :

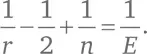
Прибавим к обеим частям 1/2:

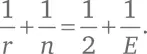
Эту формула нам скоро понадобится.

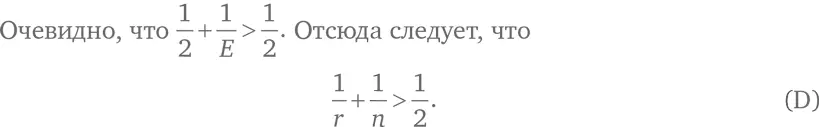
Соотношение (D) показывает, что r и n не могут быть слишком большими числами. Например, нет такой ситуации, при которой r = n = 5, потому что тогда 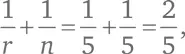что не больше 1/2. Давайте подумаем над возможными значениями r и n .

Вначале отметим, что r и n должны быть равны по меньшей мере 3. Грани – это многоугольники, и первая фигура в ряду n -угольников – треугольник. Многогранник – пространственная фигура; если r = 2, то в одной вершине встречаются всего два ребра; в случае с объемной фигурой необходимо r ≥ 3.

Переберем все возможные значения n :

Итак, есть всего 5 пар ( n, r ): (3, 3), (3, 4), (3, 5), (4, 3) и (5, 3).

Обладая значениями n и r , мы можем вычислить значение E (исходя из формулы 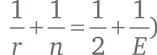и затем вывести V и F , используя формулы (B) и (C). Вот выкладки для всех пяти случаев:

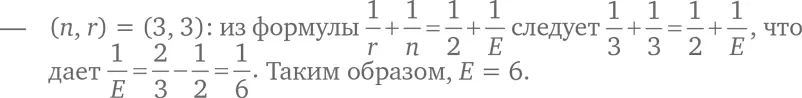
Исходя из (B), 2 E = rV . Следовательно, 12 = 3 V, и V = 4.

Исходя из (C), 2 E = nF . Следовательно, 12 = 3 F, и F = 4.

Вывод: ( n, r ) = (3, 3) означает, что ( V, E, F ) = (4, 6, 4). Единственная возможность склеить четыре равносторонних треугольника в пространственную фигуру – это тетраэдр;

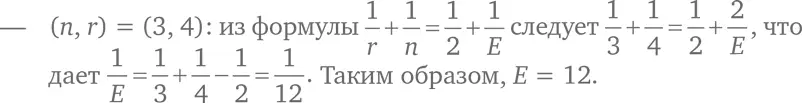
Исходя из (B), 2 E = rV . Следовательно, 24 = 4 V, и V = 6.

Исходя из (C), 2 E = nF . Следовательно, 24 = 3 F, и F = 8.

Вывод: ( n, r ) = (3, 4) означает, что ( V, E, F ) = (6, 12, 8). Единственный способ склеить восемь равносторонних треугольников в пространственную фигуру так, чтобы в каждой вершине сходились четыре ребра, – это октаэдр;

Исходя из (B), 2 E = rV . Следовательно, 60 = 5 V, и V = 12.

Исходя из (C), 2 E = nF . Следовательно, 60 = 3 F, и F = 20.

Вывод: ( n, r ) = (3, 5) означает, что ( V, E, F ) = (12, 30, 20). Единственный способ склеить 20 равносторонних треугольников так, чтобы в каждой вершине сходились пять ребер, – это икосаэдр;

– ( n, r ) = (5, 3): вычисления опять-таки похожи; ( V, E, F ) = (20, 30, 12). Единственный способ склеить 12 правильных пятиугольников так, чтобы в каждой вершине сходились 5 ребер, – это додекаэдр.

С помощью великолепной формулы Эйлера и незамысловатых алгебраических выкладок мы доказали, что не существует других правильных многогранников, кроме пяти платоновых тел!

Грани правильного многогранника должны быть одинаковыми правильными многоугольниками, но если мы ослабим это условие, обнаружится новая разновидность многогранников. Пусть грани будут по-прежнему правильными многоугольниками, но не обязательно одинакового типа. Вместо этого введем условие симметрии: многогранник должен выглядеть одинаково, какую вершину ни возьми. Будем называть такие многогранники полуправильными .

Например, мы можем изготовить призму из двух равносторонних треугольников и четырех квадратов. Вершины призмы ничем не отличаются друг от друга: в каждой сходятся два квадрата и один треугольник.

Мы можем изготовить и другие призмы. Например, соединить два правильных пятиугольника, лежащих в параллельных плоскостях, четырьмя квадратами.

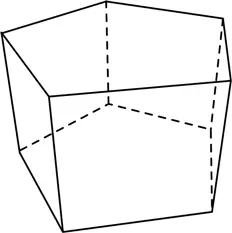
Таким образом, семейство полуправильных многогранников оказывается бесконечно большим.

Есть и другое бесконечное семейство. Возьмем два правильных n -угольника (например, два пятиугольника), лежащих в параллельных плоскостях, но слегка повернутых друг относительно друга. Соединим их вершины зигзагом и получим хоровод треугольников. Если мы правильно рассчитаем расстояние между двумя основаниями, треугольники будут равносторонними. Многогранники, построенные таким образом, называют антипризмами .

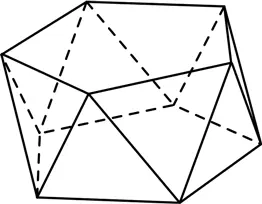
Одно из платоновых тел – призма, еще одно – антипризма. Догадываетесь, какие именно? Ответ будет в конце главы.

Призмы, антипризмы и платоновы тела – не единственные полуправильные многогранники. Ко всему прочему есть тринадцать архимедовых тел [176] Архимедовыми телами называют выпуклые многогранники, все многогранные углы которых равны, а грани представляют собой правильные многоугольники нескольких типов. – Прим. пер. . Вы легко найдете в интернете, как все они выглядят; сейчас же мы поговорим всего лишь об одном из них.