Эдвард Шейнерман - Путеводитель для влюбленных в математику

На втором этапе появляется еще девять отрезков (по три внутри каждого из трех треугольников по краям). Длина каждого маленького отрезка равна 1/4, и нам нужно прибавить к общей длине еще 9/4.

На третьем этапе возникают еще 27 отрезков (по три внутри девяти треугольников). Длина каждого равна 1/8, поэтому мы прибавляем 27/8 к итоговой длине.

Следующий этап прибавляет 81/16, и т. д. На этапе n мы прибавляем 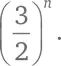Чем больше n , тем больше общая длина.

Вывод:сумма длин всех отрезков, составляющих треугольник Серпинского, бесконечна!

Треугольник Серпинского имеет нулевую площадь и бесконечную длину. Неужели у этой фигуры больше одного измерения и меньше двух? Умозаключение кажется туманным, можно выразиться поточнее. Сейчас мы покажем, что треугольник Серпинского имеет измерение 1,5849625007… Честное слово!

Количество измерений геометрической фигуры характеризует ее «толщину». Объект с одним измерением (например, отрезок) «тоньше», чем область внутри треугольника, а она, в свою очередь, «тоньше», чем шар. Посмотрим, как выразить эту расплывчатую идею «толщины» и «тонкости» на строгом математическом языке.

Идея состоит в том, чтобы начертить фигуру на миллиметровке. Мы будем рисовать одну и ту же фигуру снова и снова на бумаге со все более и более мелкой сеткой.

Проиллюстрируем эту идею с помощью незамысловатой загогулины. Изобразим одну и ту же загогулину на бумаге, размеченной клеточками 1 × 1, затем 1/2 × 1/2, затем 1/4 × 1/4 и т. д. Вот результат:

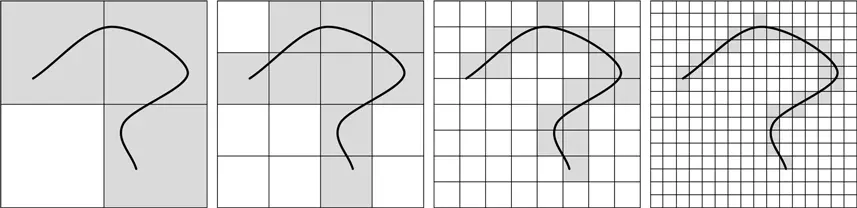
Мы закрасили клеточки, затронутые нашей кривой. Посчитаем их количество:

Заметим, что при уменьшении стороны клеточки вдвое мы, грубо говоря, удваиваем количество клеточек, необходимых для покрытия кривой. Почему так? Каждая клеточка покрывает часть длины кривой. Когда мы уменьшаем длину клеточки в два раза, нам нужно где-то в два раза больше клеточек. Это соотношение можно выразить уравнением:

Здесь N – количество клеточек, затронутых кривой, а g – длина стороны одной клеточки. Символ означает «пропорционально» и подразумевает неточность соотношения. Если бы наша кривая была обычным отрезком прямой линии, мы бы вывели точное уравнение. Но стоит ненамного скрутить прямую линию, и соотношение становится несовершенным.

Продолжим подсчитывать клеточки, на сей раз затронутые двумерной фигурой – кругом [181] Напоминаю: с точки зрения математики окружность – одномерная кривая, а круг – двумерная фигура: часть плоскости внутри окружности и сама окружность. с радиусом 1.

Будем снова и снова вычерчивать наш круг на бумаге с клеточками 1 × 1, 1/2 × 1/2, 1/4 × 1/4 и т. д. Всякий раз мы станем закрашивать клеточки, затронутые кругом, то есть те, что расположены внутри круга, и те, которые пересекает окружность.

На бумаге, расчерченной 1 × 1, разместим центр круга на перекрестье клеточек; легко заметить, что он затрагивает ровно четыре клеточки. Изобразим развитие ситуации на следующих этапах:

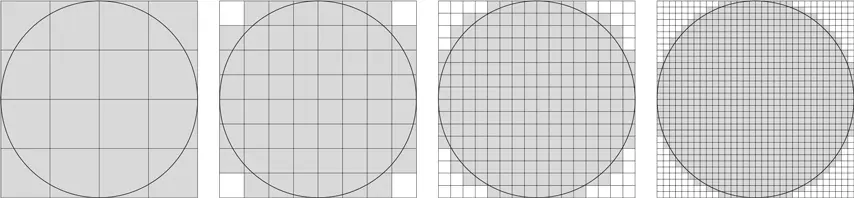
На втором этапе круг затрагивает все 16 клеточек, затем все клеточки, кроме 4, то есть 60. Считать дальше скучно, поэтому доверим процесс компьютеру. Вот результат:

Сразу видно, что уменьшение стороны клеточки в 2 раза приводит к увеличению числа закрашенных клеточек примерно в 4 раза. Вот точные соотношения:

Грубо говоря, число закрашенных клеточек действительно возрастает в четыре раза. Но это приближение становится не таким грубым, когда число клеточек увеличивается. Почему?

Когда площадь клеточек мала, подавляющее большинство закрашенных клеточек лежит внутри круга. Кое-какие можно увидеть на периферии, но их ничтожно мало по сравнению с другими. Когда мы уменьшаем сторону клеточки вдвое, клеточек внутри круга становится больше в четыре раза, а вот количество клеточек на периферии увеличивается на меньшее число, потому что часть из них окружность не пересекает.

Рассуждая таким образом, мы поймем, что уменьшение стороны клеточки в 10 раз приводит к росту числа закрашенных клеточек примерно в 100 раз. Внутри круга клеточек становится ровно в 100 раз больше, но применительно к границе это утверждение не совсем верно.

Мы можем выразить соотношение между количеством клеточек, затронутых кругом, и длиной стороны клеточки следующим образом:

Вот еще один способ убедиться в том, что формула (B) верна. Площадь круга равна π r ². Если радиус круга равен 1, его площадь равна π.

Нарисуем круг на бумаге с клеточками g × g и посчитаем, сколько клеточек он затронул; обозначим их количество буквой N . Каждая клеточка имеет площадь g ². Общая площадь закрашенных клеточек почти совпадает с площадью круга. Таким образом,

π ≈ Ng ².

Следовательно, 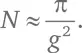В упрощенном виде это приводит к соотношению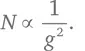

Мы нашли способ подсчитывать длины одномерных фигур и площади двумерных.

Соотношение (A) верно не только для нашей загогулины, но и для любого одномерного объекта. Когда мы делаем сетку мельче в 10 раз, количество клеточек, затронутых линией, вырастает примерно в 10 раз.

Соотношение (B) тоже выполняется не только для круга, но и для любой двумерной фигуры. Делаем сетку мельче в 10 раз – и количество клеточек, затронутых кругом, увеличивается примерно в 100 раз, потому что внутри одной большой клеточки теперь располагается 100 маленьких.

Итак: [182] Обратите внимание, что мы записали g как g 1 . Это ничего не меняет, но служит неким предзнаменованием.

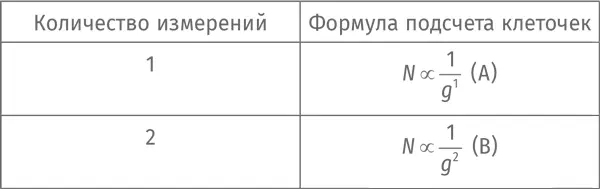
Мы теперь умеем уверенно отличать одномерные объекты от двумерных. Вычерчиваем объект на миллиметровке, делаем сетку все более мелкой и на каждом этапе подсчитываем затронутые им клеточки. Если выполняется соотношение (A), объект одномерный; если соотношение (B), объект двумерный.