Эдвард Шейнерман - Путеводитель для влюбленных в математику

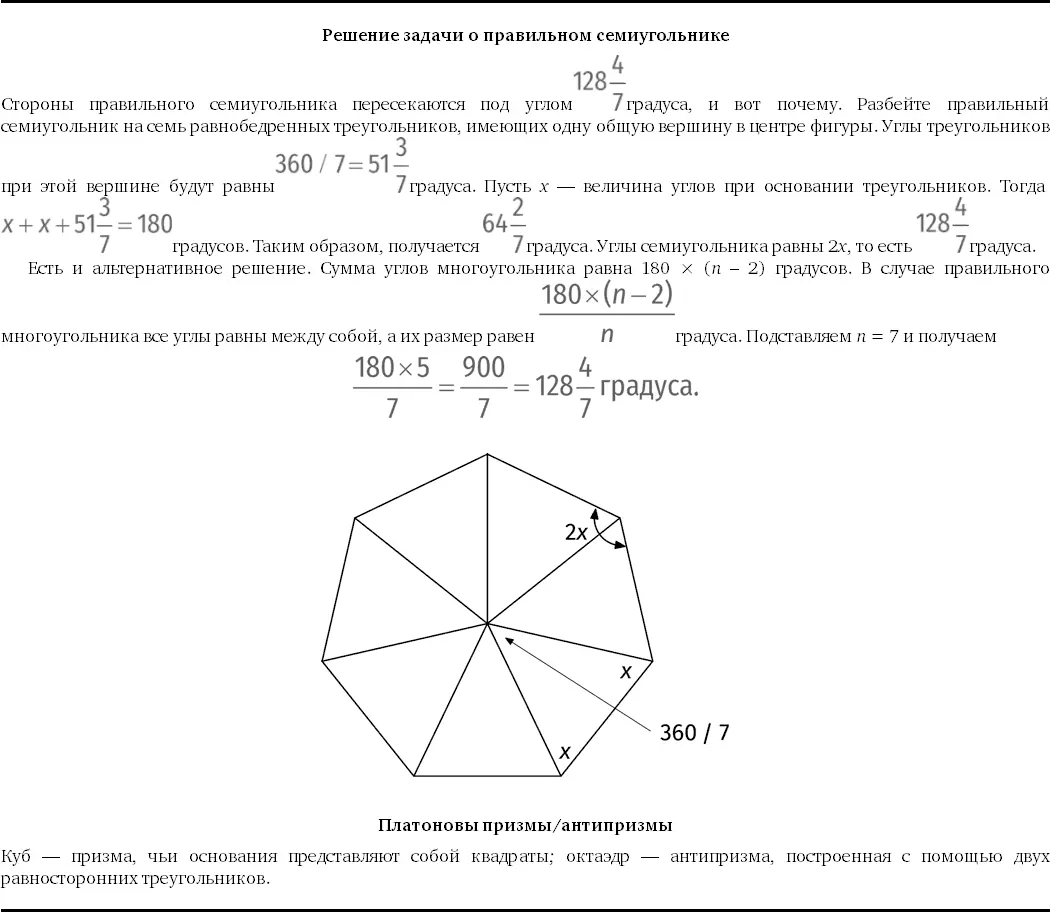
Если срезать угол икосаэдра, сечение будет иметь форму правильного пятиугольника, потому что в каждой вершине встречаются пять треугольников. Если мы срежем все 12 углов, 20 треугольных граней превратятся в шестиугольники. Если делать срезы аккуратно, стороны шестиугольников окажутся равны между собой. В итоге мы получим усеченный икосаэдр . Если мы сошьем из кожи усеченный икосаэдр, раскрасим шестиугольники белым, а пятиугольники черным и закачаем внутрь воздух, то получится футбольный мяч!

Фигуры, о которых нам рассказывали на уроках геометрии в школе, просты и понятны. Их границы четко очерчены. Все отрезки прямые, а окружности ровные. Из космоса Земля похожа на гладкую-прегладкую жемчужину, но вблизи все оказывается несколько сложнее. Крутые горные вершины возвышаются над волнистыми песчаными дюнами и бушующим океаном. Реки извиваются, леса заполнены ветвистыми деревьями. Если мы закажем художнику изобразить поверхность Земли с помощью прямых линий и дуг окружности, получится дичайший абстракционизм.

Геометрические фигуры, порожденные природой, имеют неровные границы, плохо выражаемые с помощью уравнений. Какова форма облака или пламени костра? «Начала» Евклида становятся бесполезны. Совершенно иные фигуры наполняют наш смутный изменчивый мир.

Начнем с рецепта.

Нам понадобится кусок теста и несколько чрезвычайно острых ножей. Кроме того, придется нанять побольше поваров.

Аккуратно вырежем из теста равносторонний треугольник.

Шеф-повар должен безошибочно вырезать (и выбросить) треугольник, вершины которого лежат в серединах сторон большого треугольника. Процесс изображен на рисунке.

Остаются три равносторонних треугольника. Они соприкасаются вершинами. Их площади в четыре раза меньше сторон большого треугольника.

Дальше шеф-повар вызывает трех помощников и велит им проделать такую же процедуру с треугольниками поменьше. Получится девять треугольников в 16 раз меньше большого.

Разумеется, помощники шеф-повара сами метят в шеф-повара. Каждый вызывает трех своих помощников и просит их проделать эту процедуру с маленькими треугольниками.

Процесс продолжается и продолжается. Каждый, кто участвует в нем, вызывает трех своих помощников и велит рассечь треугольники по тому же принципу. И вот что получается:

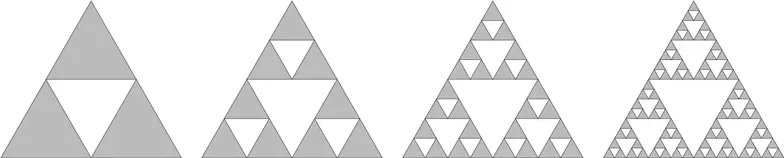
Бессчетные подручные орудуют ножами [178] Если говорить строго, мы вырезаем треугольник внутри, но не его границы; в конце концов не останется ничего, кроме этих линий. . Их становится все больше и больше, их число стремится к бесконечности. В конце концов – когда бы ни наступил этот конец – мы получим треугольник Серпинского [179] Также известен под названием «салфетка Серпинского» и «решетка Серпинского». – Прим. пер. .

Треугольник Серпинского, как и всякий фрактал, обладает двумя особенностями: он самоподобен и имеет дробную размерность .

Легко понять, что такое самоподобие. Треугольник Серпинского состоит из трех маленьких копий самого себя, а каждая из этих копий состоит из трех других копий. Когда вы вооружитесь мощнейшим микроскопом, обнаружится, что мельчайшие треугольники собраны из собственных копий. Все составные части подобны друг другу.

Но что такое дробная размерность?

Объекты в евклидовой геометрии можно рассортировать по количеству измерений.

Отрезки, дуги окружностей, границы квадратов и все такое прочее имеет одно измерение. У них есть длина, но нет толщины. Винтовая линия тоже одномерна, хотя закручивается в трехмерном пространстве.

Четырехугольники, пятиугольники, шестиугольники (на сей раз мы учитываем области внутри), круги и другие фигуры подобного рода имеют два измерения: у них есть площадь, но нет объема. Поверхность цилиндра имеет два измерения, хоти и не лежит на ровной плоскости.

Шары, кубы и другие фигуры того же класса имеют три измерения: у них есть объем.

А как насчет треугольника Серпинского? Мы начали с обычного равностороннего треугольника; видимо, у треугольника Серпинского два измерения. Но как узнать его площадь?

Для простоты будем считать, что площадь исходного треугольного куска теста равна 1 условной единице площади (например, одному квадратному сантиметру). Шеф-повар рассек треугольник на четыре одинаковых куска. Площадь выброшенного куска равна 1/4 изначальной площади; таким образом, на первом шаге площадь нашей фигуры равна 3/4 квадратного сантиметра.

Три помощника шеф-повара вырезали еще 1/4 площади, осталось 3/4 от 3/4 площади самого большого треугольника. Помощники помощников шеф-повара вырезали еще 1/4… Иными словами, на этапе n остается 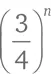начальной площади.

После 16 этапов около 99 % площади исчезнет. Если устремить n к бесконечности, вся площадь уничтожится; останутся лишь границы треугольников, у которых нет никакой площади.

Получается, у треугольника Серпинского одно измерение? Если так, то попробуем вычислить его длину.

Начнем сразу с пустого треугольника. Дальше добавляются три отрезка, соединяющих середины сторон треугольника. Повторим эту процедуру с тремя треугольниками по краям, не трогая треугольник по центру. Мы будем множить треугольники снова и снова следующим образом:

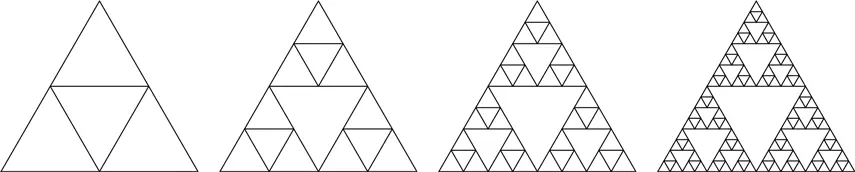
Для удобства расчетов будем считать, что длина стороны большого треугольника равна 1 условной единице [180] Обратите внимание, что площадь равностороннего треугольника со стороной 1 не равна 1. Для удобства вычислений мы рассматриваем другой треугольник. . Таким образом, сумма длин его сторон составляет 3.

Новый треугольник внутри большого добавляет три отрезка, длина каждого равна 1/2. То есть на первом этапе общая длина возрастает на 3/2.