Эдвард Шейнерман - Путеводитель для влюбленных в математику

Посмотрим, что произойдет с треугольником Серпинского на клетчатой бумаге [183] Ранее мы брали за основу равносторонний треугольник. Но он не помещается в квадрат. Поэтому будем рассматривать равнобедренный треугольник с основанием и высотой, равными 1. Принцип построения остается прежним. . Уместим его в клеточку 1 × 1. На рисунке показано, что будет при уменьшении размера клеточек до 1/2, 1/4, 1/8 и 1/16:

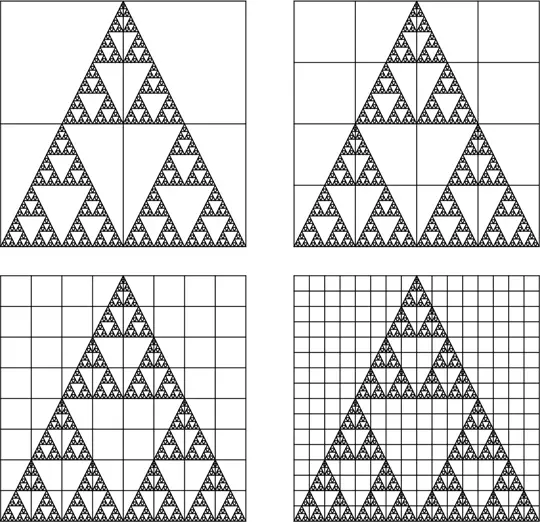
В первом случае затронуты все 4 клеточки. Во втором случае не затронуты 2 клеточки слева сверху и 2 клеточки справа сверху, а всего клеточек 16 штук. Вот таблица целиком:

Вопрос:когда мы уменьшаем сторону клеточки вдвое, количество клеточек, затронутых нашей фигурой, увеличивается в два раза (случай одномерного объекта) или в четыре раза (случай двумерного объекта)?

Разумеется, вся соль в том, что ни один из двух вариантов не подходит. На новом этапе количество клеточек вырастает ровно в три раза [184] Увеличение числа клеточек в три раза вытекает из самоподобия треугольника Серпинского. Посмотрите на квадрат с 16 клеточками. Легко заметить, что треугольник Серпинского захватывает 12 клеточек. Теперь посмотрите на следующий квадрат, но не спешите подсчитывать клеточки. Просто обратите внимание, что новый треугольник состоит из трех уменьшенных копий предыдущего. Каждая из них захватывает всё те же 12 клеточек. Общее число клеточек 36. Когда вы переведете взгляд на следующий квадрат, вы снова обнаружите три копии предыдущего треугольника. Очевидно, что они захватывают 108 клеточек. . Их число растет быстрее, чем в случае одномерных объектов, но медленнее, чем в случае двумерных. Таким образом, размерность треугольника Серпинского лежит между двумя целыми величинами.

Мы можем в точности вычислить размерность треугольника Серпинского, но это потребует базовых знаний о логарифмах и некоторых алгебраических выкладок. Если вам все это в тягость, можете спокойно пропустить следующие абзацы.

Итак, цель состоит в том, чтобы найти формулу вроде (A) или (B): Число d в ней и будет количеством измерений нашей фигуры.

Если сторона клеточки равна (где k – натуральное число), то Вот проверка:

Формула дает в точности те же числа, что и в предыдущей таблице.

Задача состоит в том, чтобы найти такое число d , что Прологарифмируем обе части [185] Символ ~ означает примерное равенство, точность которого возрастает с ростом величины переменных. :

Мы знаем Подстановка в предыдущую формулу дает:

Наряду с треугольником Серпинского существует ковер Серпинского. Вот этапы его построения:

Устремляясь к бесконечности, мы получим такую картинку:

Как вы думаете, какова размерность этого фрактала? Ответ вы найдете в конце главы.

Студенты на факультетах математики до потери пульса разлагают на множители полиномы, в первую очередь степени x + y . Восстановим в памяти, о чем идет речь:

Мы можем расположить коэффициенты данных полиномов в таблице. Ее называют треугольником Паскаля :

Мы расположили эти числа по квадратам, а теперь давайте раскрасим некоторые из них черным цветом. Пусть квадраты с нечетными числами станут черными, а квадраты с четными останутся белыми:

Продолжим вплоть до 64 ряда. Как вы думаете, что получится?

Разве это не великолепно?

Я хочу завершить главу, посвященную фракталам, рассказом о неотразимой фигуре, придуманной Хельге фон Кохом [186] Нильс Фабиан Хельге фон Кох (1870–1924) – шведский математик, специалист по теории чисел. Статья о снежинке Коха вышла в 1904 году. Это один из первых изученных фракталов. – Прим. пер. . Алгоритм ее построения чрезвычайно прост. Мы начинаем с прямого отрезка, делим его на три части и строим равносторонний треугольник на основе среднего из трех новых отрезков. Затем мы удаляем центральный отрезок. Теперь у нас есть четыре отрезка, каждый из которых в три раза меньше исходного. Мы повторяем процедуру с каждым из этих отрезков.

Чтобы получить снежинку целиком, начнем с равностороннего треугольника и проделаем описанную процедуру с каждой из его сторон. Это выглядит следующим образом:

Устремляясь к бесконечности, мы получим снежинку Коха.