Эдвард Шейнерман - Путеводитель для влюбленных в математику

Прямая представляет собой множество точек, как и окружность или треугольник. Это множество точек обладает определенными свойствами.

Интуитивно мы понимаем, что такое прямая: она тонкая (у нее нет толщины), ровная и бесконечно продолжается в обоих направлениях. Но такое описание – еще не математическое определение. Чем прямая линия отличается от кривой? Закрепить эту идею не так-то просто.

Как мы уже отмечали, у Евклида был собственный подход к определению базовых объектов, сегодня мы воспринимаем точки и прямые иначе. У нас есть объекты под названием «точки» и множества этих объектов под названием «прямые». Если оба рода объектов удовлетворяют постулатам Евклида, получается система под названием евклидова геометрия .

Если мы изменим утверждения Евклида о фундаментальных свойствах точек и прямых, мы получим геометрию иного типа. Рассмотрим простой пример. Для начала мы сохраним первый постулат Евклида, который гласит:

1. Если даны две точки, есть одна и только одна прямая, проходящая через эти точки.

А дальше включим новый постулат, переворачивающий роли прямых и точек:

1'. Если даны две прямые, есть одна и только одна точка, принадлежащая данным двум прямым [192] Таким образом, параллельных прямых в этой системе не существует: всякая пара прямых имеет точку пересечения. Это разительное отличие от евклидовой геометрии. .

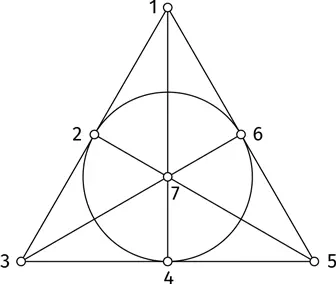
Должным образом выбранные «точки» и «прямые» могут удовлетворить тому и другому условию. Пусть у нас есть семь точек. Назовем их незамысловатым образом: 1, 2, 3, 4, 5, 6 и 7. Кроме того, у нас есть семь прямых: {1, 2, 3}, {1, 5, 6}, {1, 4, 7}, {2, 5, 7}, {2, 4, 6}, {3, 4, 5} и {3, 6, 7}.

Эти «прямые» не имеют ничего общего с «прямыми» Евклида [193] Система из семи точек и семи прямых называется плоскостью Фано. . Каждая состоит всего из трех точек!

Мы легко удостоверимся, что в этой системе из семи точек и семи прямых верны оба постулата.

• Проверим постулат 1. Возьмем любые две точки, скажем 2 и 5. Они принадлежат прямой {2, 5, 7}, и нет другой прямой, содержащей эти две точки. Вы можете самостоятельно рассмотреть все пары среди семи точек и увидеть, что всегда есть прямая, и только одна, содержащая обе точки.

• Проверим постулат 1'. Выберем любые две прямые, например {1, 4, 7} и {3, 4, 5}. Обе содержат точку 4, и это единственная общая для них точка. Вы можете рассмотреть все пары среди семи прямых и увидеть, что они всегда имеют общую точку, причем всего одну.

Странно рассуждать о геометрии без чертежей. К счастью, можно изобразить данную систему с помощью диаграммы. Семь точек помечены кружочками, а прямые представляют собой отрезки (в большинстве случаев) и окружность (в случае прямой {2, 4, 6}).

Хитрость заключается в том, что мы подобрали некие объекты, назвали их «точками», а затем по определенному принципу сформировали множества этих объектов и назвали их «прямыми». Если все объекты удовлетворяют нашим постулатам, мы по праву можем называть их точками и прямыми, даже если они не имеют ничего общего с точками и прямыми в понимании Евклида.

Евклидовы точки и линии можно определить следующим образом. Точка – пара действительных чисел ( x, y ). Прямая – множество точек ( x, y ), удовлетворяющих уравнению ax + bx + c = 0, где числа a и b не равны нулю. С помощью этих определений (и соответствующих определений окружности и угла) можно доказать , что постулаты Евклида выполняются.

Если мы воспринимаем точки как пары чисел, а прямые как решения уравнений, то оказываемся на декартовой плоскости, названной в честь математика и философа Рене Декарта.

Мы стали своевольничать с употреблением слов «точка» и «прямая». Мы можем назвать что угодно «точкой» и сгруппировать эти точки в множества под названием «прямые», если все они удовлетворяют надлежащим постулатам. Что значит надлежащим ? Для Евклида несомненными утверждениями были те пять постулатов, которые мы привели в начале главы.

Я сейчас расскажу о новых определениях «точек» и «прямых», необходимых для создания гиперболической геометрии . В этой геометрии все точки лежат внутри одной окружности. Область внутри нее мы будем называть гиперболической плоскостью [194] Эту модель гиперболической плоскости называют диском Пуанкаре в честь французского математика Анри Пуанкаре (1854–1912). .

Прямые на гиперболической плоскости представляют собой дуги окружностей. Это обескураживает: как дуга может быть прямой? Разве дуга не кривая? Давайте говорить «гиперболическая прямая» , отличать ее от негибкой тезки.

Вот два способа построения гиперболических прямых:

• Начертите окружность, пересекающую гиперболическую плоскость под двумя прямыми углами. Часть окружности внутри гиперболической плоскости представляет собой гиперболическую прямую.

• Проведите прямую через центр гиперболической плоскости. Часть прямой внутри гиперболической плоскости тоже представляет собой гиперболическую прямую.

На чертеже вы можете видеть три прямые на гиперболической плоскости.

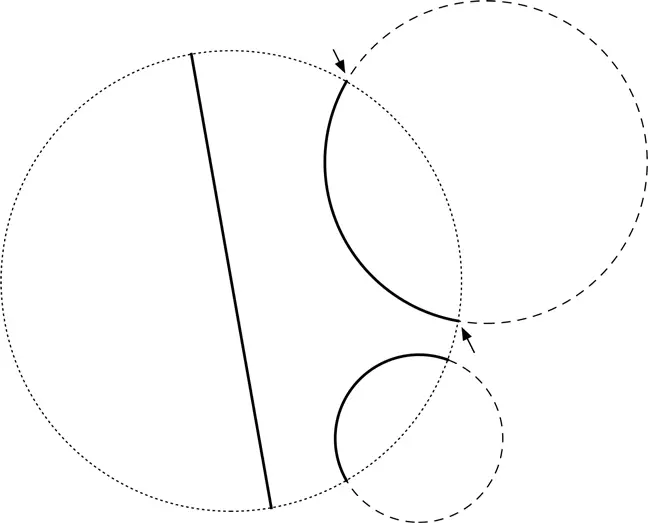
Гиперболическая плоскость – это область внутри обозначенной точками окружности. Две гиперболические прямые – дуги пунктирных окружностей, еще одна гиперболическая прямая – диаметр окружности, обозначенной точками. Замечу, что конечные точки дуг и диаметра не относятся к соответствующим гиперболическим прямым. (Обозначенные пунктиром окружности не входят в гиперболическую плоскость, они просто показывают, по какому принципу мы вычерчиваем гиперболические прямые – это части окружностей, пересекающих обозначенную точками окружность под прямыми углами.)

На следующем чертеже вы видите три гиперболические прямые. Две из них пересекаются, а третья параллельна и той и другой! Такое совершенно невозможно на евклидовой плоскости.

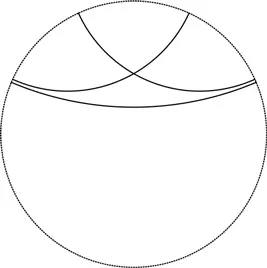
Здесь все не так, как мы привыкли. Многие геометрические «факты» на евклидовой плоскости не работают в случае гиперболической плоскости.

Для начала: все не так с треугольниками. На евклидовой плоскости сумма углов треугольника равна 180° (мы доказали это обстоятельство в главе 13, однако опирались на постулат о параллельных прямых). На гиперболической плоскости сумма углов треугольника меньше 180°.