Эдвард Шейнерман - Путеводитель для влюбленных в математику

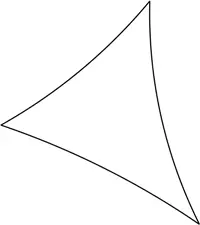
На евклидовой плоскости площадь треугольника может быть настолько большой, насколько мы того хотим. На гиперболической плоскости максимальная площадь треугольника не может превышать некоторой величины, и есть простая формула для подсчета площади. Если сумма углов треугольника равна s, площадь треугольника равна K × (180 – s ), где K – определенное число [195] Если мы возьмем другой масштаб евклидовой плоскости, она не изменится. Гиперболическая плоскость, напротив, преображается при смене масштаба. Число K зависит от него. . В соответствии с этой формулой два разных треугольника с равными углами имеют равную площадь. В евклидовой геометрии это не так: скажем, треугольники с углами 35°, 60° и 80° имеют одну и ту же форму (другими словами, подобны ), но не обязательно совпадают по размеру. На гиперболической плоскости два треугольника с углами 35°, 60° и 80° не просто совпадают по площади – они конгруэнтны!

Квадрат – это четырехугольник, в котором все углы равны 90°. Вот интересный факт о квадратах на гиперболической плоскости: их попросту не существует ! На рисунке изображена фигура на гиперболической плоскости, у которой три угла равны 90°, а четвертый меньше 90°.

Почему прямоугольников здесь нет? Подумаем о четырехугольнике R на гиперболической плоскости. Рассечем его на две части по линии, соединяющей два противоположных угла. Получатся два треугольника. Сумма углов в каждом меньше 180°, поэтому сумма углов образованного ими четырехугольника меньше 360°. Следовательно, все четыре угла не могут быть равны 90°.

Можно замостить евклидову плоскость равносторонними треугольниками или шестиугольниками [196] Разбиение плоскости на многоугольники в математики называют паркетом, мозаикой или замощением. Здесь мы обсуждаем замощение плоскости правильными n -угольниками. . Однако нельзя замостить ее правильными пятиугольниками. Почему? Углы правильного пятиугольника равны 108°. Углы при общей вершине трех правильных пятиугольников дают в сумме 324°, что меньше полного угла. Остается зазор. Четыре правильных пятиугольника не могут иметь общую вершину, в противном случае углы при ней давали бы в сумме 432°, что превышает 360°.

В то же время углы правильного n -угольника на гиперболической плоскости зависят не только от n . Мы можем построить правильный пятиугольник, все углы которого равны 90° (посмотрите на иллюстрацию).

Углы при общей вершине четырех таких пятиугольников дают в сумме ровно 360°. Таким образом, ими можно замостить всю гиперболическую плоскость, как показано на рисунке.

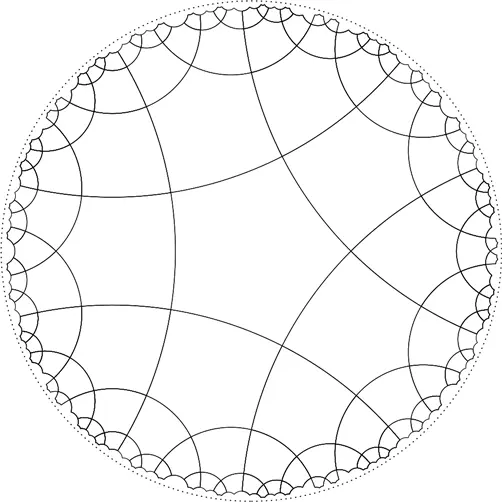
Все пятиугольники на рисунке совпадают по размеру и по форме. Они выглядят все меньше и меньше, приближаясь к границе, но это всего лишь особенность изображения гиперболической плоскости. На самом деле все «паркетины» на иллюстрации абсолютно идентичны. Это правильные многоугольники с пятью углами по 90° каждый, и их можно плотно пригнать друг к другу [197] Замощение гиперболической плоскости вдохновляло многих художников, среди них наиболее известен Мауриц Эшер. .

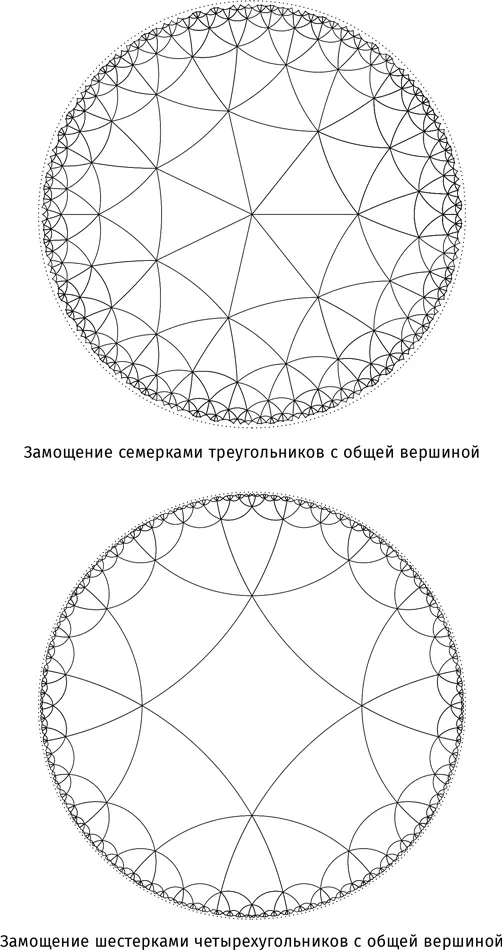
Вот еще два примера замощения гиперболической плоскости для услаждения ваших глаз.

Мир одержим выстраиванием рейтингов. Мы составляем рейтинги атлетов, спортивных команд, больниц, ресторанов, фильмов, поп-музыки, студентов, коллег, городов, работы, машин, и т. д., и т. д. Нам нравится знать «самое-самое» – то, что входит в «первую десятку».

Это все чепуха, забавная чепуха, но тем не менее. Среди прочего чепуха происходит от того, насколько субъективна методология оценки. Если определенный ресторан в вашем городе признан лучшим, это не обязательно ваш любимый ресторан. Ваши предпочтения могут отличаться от суждений ресторанных критиков, а их взгляды на один и тот же вопрос зачастую прямо противоположны.

Можно выбрать объективную систему оценивания и все равно получать ничтожные результаты: например, оценивать фильмы по сумме выручки от их проката – это объективно и поддается подсчету. Можно аргументировано доказать: чем лучше фильм, тем больше людей жаждут заплатить за то, чтобы увидеть его. Но бывает такое, что фильм, сорвавший кассу, навевает на вас скуку, а малобюджетный инди-фильм [199] Инди-культура (от англ. independent – «независимый») противопоставляет себя коммерческому мейнстриму. – Прим. пер. западает в душу. Выручка от проката обычно говорит скорее о маркетинге, а не качестве картины.

Но, предположим, мы преодолели субъективность и достигли всеобщего соглашения относительно того, как сравнивать конкурентов. Попробуем выпарить идею ранжирования до ее математической сути. Улетучится ли тогда вся чепуха?

Сыграем в простую игру. Каждый бросит кубик, и у кого выпадет больше очков, тот выиграет. Если мы возьмем два обыкновенных кубика, где грани пронумерованы от одного до шести, то нет смысла говорить, что одна чем-то лучше другой. Они одинаковые.

Теперь сменим числа на гранях. Назовем наши игральные кости A и B .

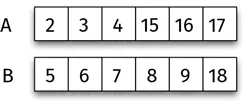
Какая из них лучше, A или B ? Какую вы предпочтете?

Для того чтобы ответить на этот вопрос, рассмотрим все вероятности: как могут выпасть игральные кости? Если игральная кость A выпала числом 2 вверх, то для сравнения есть шесть вариантов того, как может выпасть игральная кость B . Если выпало число 3, вариантов для сравнения опять-таки шесть. Таким образом, есть 6 + 6 + 6 + 6 + 6 + 6 = 6 × 6 = 36 возможностей, и все они равновероятны. Иногда побеждает обладатель игральной кости A , иногда – обладатель игральной кости B (все числа на гранях разные, поэтому нет варианта сыграть раунд вничью). Кто выигрывает чаще?