Эдвард Шейнерман - Путеводитель для влюбленных в математику

P ( S ∧ T ) = P ( T ∧ S ) = P ( T | S ) × P ( S ) = 0,98 × 0,001 = 0,00098.

Теперь вычислим P ( T ). Нам известно, что 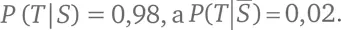В то же время Далее:

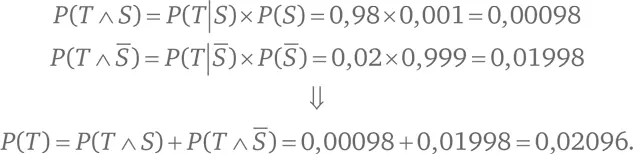
Применим формулу Байеса в последний раз:

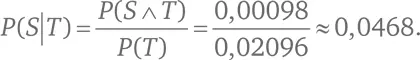
Это совпадает с нашими предыдущими вычислениями.

Что делает событие непредсказуемым? Предыдущие главы были посвящены понятию вероятности . Центральная идея теории вероятностей заключается в том, что некоторые феномены случайны : их нельзя предсказать в точности, поскольку они недетерминированы . Разумно и эффективно рассматривать некоторые феномены внешнего мира, такие как вращение брошенного кубика, в качестве случайных.

Но случаен ли бросок костей в действительности? Возможно, если мы детально знаем все характеристики кубика – от скорости вращения в зависимости от плотности воздуха в комнате до коэффициента трения о поверхность стола, мы сумеем в точности определить, какой гранью вверх он остановится. Возможно, вращение кубика не случайно – просто это чрезвычайно сложное явление.

Есть ли что-нибудь случайное? Физики утверждают, что некоторые феномены действительно непредсказуемы; таков основополагающий принцип квантовой механики. Поведение элементарных частиц, таких как электрон и фотон, нельзя предсказать, поскольку неопределенность – одно из их фундаментальных свойств.

Другие физические, биологические и социальные феномены могут быть чрезвычайно хорошо смоделированы с помощью теории вероятностей. Это потрясающе. Но насколько они случайны? Не исключено, что они чересчур сложны для понимания.

Так возникает главный вопрос этой главы: может ли система быть простой, полностью детерминированной, но все же непредсказуемой?

Ключевая идея этой главы – итерация функций. Под итерацией мы подразумеваем повторение одной и той же операции снова и снова. Что математики подразумевают под функцией ?

Функции можно рассматривать в качестве своего рода «черных ящиков», преобразующих одно число в другое [208] В фокусе нашего внимания только те функции, которые преобразуют числа в числа. В целом функции превращают любые математические объекты в любые математические объекты. . Вообразим, что у черного ящика есть входной лоток, куда мы засыпаем числа, дальше мы крутим ручку, машина делает свое дело, и на выходе из ящика вываливаются новые числа.

Например, представим себе ящик, выполняющий следующую операцию. Мы бросаем туда число, он возводит его в квадрат, добавляет к результату единичку и выплевывает то, что получилось. Дадим этой функции имя; назовем ее «возведи в квадрат и прибавь один». Вот как она работает с числом 3:

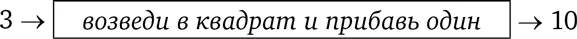
Описывать действия функции словами обременительно, гораздо проще использовать математические символы. Что касается числа 3, мы вначале возводим его в квадрат: 3² = 9, а затем прибавляем единичку: 3² + 1 = 10. Как будет выглядеть результат с числом 4? Очевидным образом, 4² + 1 = 17.

Вместо длинных имен (вроде «возведи-в-квадрат-и-прибавь-один»), математики обозначают функцию какой-нибудь буквой, чаще всего f . Число, с которым имеет дело функция, помещают в круглые скобки сразу за буквой, например: f (4).

Эта форма записи удобна для описания функции:

f ( x ) = x ² + 1.

Это значит, что функция превращает число x в число x ² + 1.

Вот еще один пример. Определим новую функцию g таким образом:

g ( x ) = 1 + x + x ².

Чему равно g (3)? Мы подставляем число 3 в формулу и получаем:

g (3) = 1 + 3 + 3² = 13.

Функции можно комбинировать, чтобы одна операция следовала за другой. Подумаем, чему равно f ( g (2)).

Это выражение вынуждает нас вычислить функцию f от какой-то величины. От какой? Она зависит от того, чему равно g (2). А чему оно равно? g (2) = 1 + 2 + 2² = 7. А теперь посчитаем f (7) = 7² + 1 = 50. Если уложить всё в одну строчку, получится:

f ( g (2)) = f (7) = 50.

Давайте проверим, хорошо ли вы усвоили материал. Посчитайте g ( f (2)). Это не 50! Верный ответ – в конце главы.

Вернемся к определению итерации. Как я уже сказал, итерация означает просто повторение одной и той же операции снова и снова. Еще раз: итерация означает просто повторение одной и той же операции снова и снова. Еще раз: итерация означает просто повторение… (Окей, надеюсь, вы уловили юмор.)

Подумаем о функции f ( x ) = x ² + 1. Запись f ( f ( x )) означает, что мы применяем операцию f дважды: берем число x , закидываем его в функцию f , а потом снова закидываем то, что получилось, в функцию f . Вот пример:

f ( f (2)) = f (2² + 1) = f (5) = 5² + 1 = 26.

Можно проводить итерацию сколько угодно раз. Например, трижды:

f ( f ( f (2))) = f ( f (5)) = f (26) = 26² + 1 = 677.

Когда мы выходим на четвертую итерацию, запись становится громоздкой. Поэтому вместо f ( f ( f ( f ( x )))) мы будем записывать f ⁴( x ), подразумевая, что верхний индекс означает не возведение в степень, а последовательное применение функции. Для положительного целого числа n выражение f n( x ) означает:

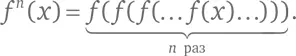
Сейчас мы проитерируем функции вида f ( x ) = mх (1 – х ), где m – некое число. Это семейство функций называется логистическим отображением [209] Отображение – просто синоним термина «функция». . Во всех случаях мы будем начинать с числа x = 0,1, итерировать функцию и наблюдать за происходящим. Мы начнем с функции:

f ( x ) = 2,5 x (1 – x ).

Начнем с x = 0,1 и на первом шаге посчитаем:

f (0,1) = 2,5 × 0,1 × (1–0,1) = 2,5 × 0,1 × 0,9 = 0,225.

Применим f снова:

f ²(0,1) = f (0,225) = 2,5 × 0,225 × (1–0,225) = 2,5 × 0,225 × 0,775 = 0,4359375.