Эдвард Шейнерман - Путеводитель для влюбленных в математику

Гипотеза Коллатца [213] Лотар Коллатц выдвинул эту гипотезу в 1937 году. заключалась в том, что вне зависимости от того, с какого целого положительного числа x мы начинаем, последовательность итераций рано или поздно достигает единицы и тройка 4 → 2 → 1 повторяется до бесконечности.

Проблема была решена самым умопомрачительным образом – штурм потребовал чудовищной дотошности математиков-профессионалов и математиков-любителей.

Демократия – процесс, основанный на предпочтениях членов общества. Людям дают возможность выразить свое мнение (путем голосования) и затем учитывают их голоса, когда принимают окончательное решение.

Знакомая всем демократическая процедура – выборы, на которых два кандидата претендуют на одну и ту же должность. Избиратели отдают голоса за первого или второго кандидата, и побеждает тот, кто наберет больше голосов.

Ключевая фраза: побеждает тот, кто наберет больше голосов – краеугольный камень демократического общества. Но насколько справедлив этот принцип?

Вообразим, что два кандидата, претендующих на одну и ту же должность, зовутся A и B. Избиратели отдают голос за того или другого [214] Более сложная система выборов подразумевает, что избиратели отмечают, насколько сильно они предпочитают одного кандидата другому. . Если отдано n голосов, данные голосования выглядят следующим образом [215] Мы будем использовать термин «профиль предпочтений» для совокупности индивидуальных голосов. :

Как используется такой профиль предпочтений для принятия решения? Обычно просто подсчитывают, сколько голосов было отдано за каждого кандидата. Победителем оказывается тот, кто набрал больше голосов. Мы назовем такой подход правилом большинства – это метод демократических сообществ. Но это не единственный метод учета профиля предпочтений для принятия решения. Посмотрим на альтернативы.

Правило диктатораподразумевает, что решение принимается на основе голоса одного-единственного человека, скажем избирателя № 1. Если № 1 выбирает A, побеждает A; если № 1 выбирает B, побеждает B. Другие мнения не учитываются.

Мы будем называть правило большинстваи правило диктатора методами принятия решений . На входе – голоса избирателей, на выходе – решение о победе того или другого кандидата. В мире используют оба метода, но правило диктаторасчитается нечестным. Почему?

Для вящей справедливости метод принятия решения должен обладать определенными свойствами. Обидная особенность правила диктаторазаключается в том, что голоса не учитываются равным образом. Более формально: справедливый метод принятия решения должен следовать нейтральности учета голосов [216] Важно не смешивать метод принятия решения (например, правило большинства ) со свойствами, которыми он обладает (например, нейтральность учета голосов ). Разные методы могут обладать каким-то одним свойством, но отличаться другими. Мы высвечиваем разницу, используя полужирное начертание для обозначения метода и курсив для обозначения свойства. – не важно, кто голосует, важно, сколько голосов отдано за того или другого кандидата. Правило большинстваотвечает требованию нейтральности учета голосов , а правило диктатора – нет.

Если мы руководствуется только теми методами, которые обладают свойством нейтральности учета голосов , мы просто суммируем голоса, отданные за того или другого кандидата. Итоговая статистика может выглядеть следующим образом:

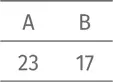
Есть и другой метод. Назовем его правилом алфавита. Побеждает тот кандидат, чье имя идет первым по алфавиту. Тогда в любом случае побеждает кандидат A.

Очевидно, и этот метод несправедлив, но почему?

Он обладает свойством нейтральности учета голосов : все избиратели равны в том плане, что не учитывается ничье мнение! Проблема состоит в том, что кандидаты поставлены в неравное положение. Мы будем говорить, что метод обладает свойством нейтральности учета кандидатов [217] Отмечу, что правило диктатора удовлетворяет требованию нейтральности учета кандидатов . , если к кандидатам относятся одинаково; если кандидат сменит имя, это не повлияет на итог выборов.

Чувство справедливости требует нейтральности учета голосов и нейтральности учета кандидатов . Достаточно ли этого?

Есть еще один метод, который мы будем называть правилом нечетности: победу одерживает тот кандидат, который набрал нечетное число голосов. Если A предпочли 20 избирателей, а B – 13 избирателей, побеждает B. Этот метод отвечает требованиям нейтральности учета голосов и нейтральности учета кандидатов .

Или рассмотрим правило меньшинства: побеждает тот, кто набрал меньше всего голосов. Если A предпочли 12 избирателей, а B – 30 избирателей, побеждает A. Этот метод также отвечает требованиям нейтральности учета голосов и нейтральности учета кандидатов .

Два требования, нейтральность учета голосов и нейтральность учета кандидатов , исключают некоторые нечестные методы (такие как правило диктатораи правило алфавита), но кое-какие несуразные методы отвечают тому и другому требованию. Введем новое свойство, позволяющее отсеять разумные методы (такие как правило большинства) от несуразных.

Вот в чем заключается проблема с правилом нечетности. Вообразим, что профиль предпочтений следующий:

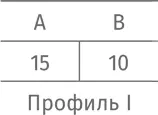
Если руководствоваться правилом нечетности, побеждает A.

Теперь предположим, что один избиратель передумал, забрал свой голос за B (проигравшего) и отдал A (победителю). Передумал всего лишь один избиратель; другие остаются при своем мнении. Итог таков:

Правило нечетностиприводит B к победе.

Нечестно! Если один избиратель меняет свое мнение и предпочитает победителя проигравшему, это не должно влиять на результат. Правило нечетностинарушает требование монотонности [218] Вот формальное определение монотонности . Мы называем метод принятия решений монотонным, если перемена решения одного избирателя в пользу победителя не меняет итога выборов. .