Эдвард Шейнерман - Путеводитель для влюбленных в математику

Есть еще одна проблема с правилом нечетности. Что произойдет, если избирателей четное количество? Рассмотрим две ситуации:

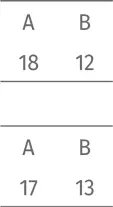
В первом случае победителей нет, во втором случае побеждают оба кандидата. В том или ином случае мы заходим в тупик.

Желательно избегать тупиковых итогов на выборах, чтобы коллективное мнение избирателей приводило к определенному решению. Некоторые методы (такие как правило диктатора) никогда не создают таких проблем. Но некоторые методы, отвечающие требованиям нейтральности учета голосов и нейтральности учета кандидатов , тоже могут завести в тупик: например, если голоса избирателей распределились поровну.

Даже если мы накладываем условия нейтральности учета голосов и нейтральности учета кандидатов, половина голосов может уйти первому кандидату, а другая половина – второму, так что нельзя будет принять внятное решение. Такое вероятно даже в случае правила большинства.

Однако оно не позволяет выбрать победителя в одной-единственной ситуации. Мы будем говорить, что этот метод в целом однозначный , так как позволяет принять решение во всех случаях, кроме одного: когда голоса распределились поровну [219] Правило диктатора, конечно, однозначное: оно никогда не заводит в тупик. .

Правило меньшинстватоже в целом однозначное (но не монотонное ).

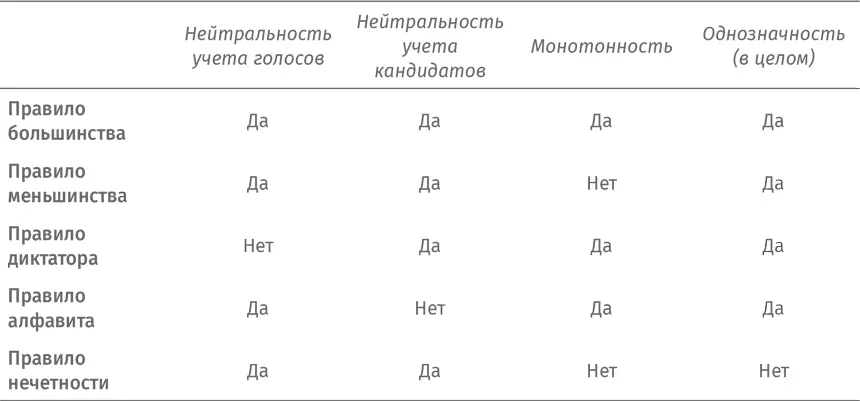
Мы определили четыре свойства справедливых выборов: нейтральность учета голосов, нейтральность учета кандидатов, монотонность и однозначность . К счастью, правило большинстваобладает всеми этими свойствами. Занесем результаты в таблицу:

Но ведь должны быть альтернативы! Есть ли другие методы принятия решений, отвечающие всем четырем требованиям?

Ответ отрицательный. В 1952 году Кеннет Мэй [220] Кеннет Мэй (1915–1977) – американский математик, экономист и историк математики. Защитил диссертацию по математической теории трудоустройства. Придерживался коммунистических взглядов. – Прим. пер. доказал, что правило большинства – единственный метод, обладающий всеми четырьмя свойствами [221] В терминологии Мэя – нейтральность, анонимность, положительный отклик и однозначность. – Прим. пер. .

Наше интуитивное предчувствие, что правило большинствасправедливее всего, подтвердилось со всей математической строгостью. Теорема Мэя говорит о том, что для выборов в случае двух кандидатов есть всего лишь один разумный метод.

Ситуация существенно меняется, если число кандидатов возрастает. Но мы все еще вправе надеяться, что методы вроде правила большинстваостаются эффективны.

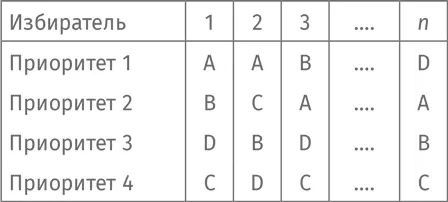
Начнем с описания того, как именно избиратели отдают голоса. Если кандидатуры выдвинули три (или больше) человека, каждый избиратель должен ранжировать их в своем бюллетене [223] Я максимально упрощаю ситуацию Можно себе представить, что избиратель симпатизирует A, равнодушен к B и C и полностью отвергает кандидатуру D. Так или иначе, мы рассчитываем, что избиратель все-таки ранжирует их. Математики рассматривают более сложные ситуации, но мы с вами ограничимся самой простой моделью. . Статистика может выглядеть так:

Как и раньше, мы ищем методы принятия решений, учитывающие распределение голосов на входе, а на выходе выносящие решение о победителе.

Например, правило диктатораподразумевает, что победа достанется тому, кто возглавляет список предпочтений одного-единственного избирателя № 1. В нашем случае это кандидат A. Прочие голоса игнорируются.

Правило диктаторане отвечает требованию нейтральности учета голосов (хотя требование нейтральности учета кандидатов здесь выполняется). Вероятно, разумнее руководствоваться методами, нейтрально учитывающими голоса, и посчитать, каков приоритет того или иного кандидата для каждого избирателя. Например, в случае трех кандидатов [224] Если в выборах участвуют k кандидатов, существует k ! возможностей распределения приоритетов (см. главу 10). итоговая статистика выглядит так:

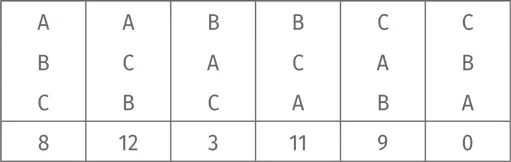
Согласно этой статистике, 20 человек поставили на первое место A, 14 предпочли B, 9 предпочли C. Как нам выбрать победителя?

Правило большинствахорошо подходит, когда кандидатов двое. В случае трех кандидатов перевес возникает тогда, когда больше половины избирателей поставили на первое место одного кандидата. Это происходит не всегда, потому руководствоваться правилом большинствастановится проблематично. Кроме того, правило большинстване учитывает распределение приоритетов второй и третьей степени. Посмотрим, насколько это важно. Проанализируем следующий профиль предпочтений:

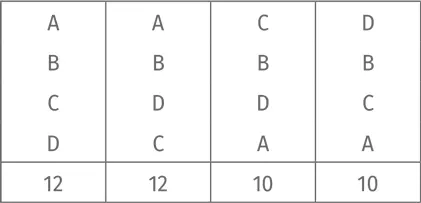
Отмечу, что больше половины избирателей поставили на первое место A. Следует ли из этого, что отдать победу A – лучший выбор? А что значит «лучший»? Математика ответить не в силах. Для нас справедливо то, что соответствует нашей системе ценностей. Проиллюстрируем это обстоятельство. Вообразим, что «кандидаты» у нас – рестораны, а «избиратели» – офисные клерки, ищущие место для проведения корпоратива. Вот информация о ресторанах:

Ситуация вполне реальная. Большинство клерков (24 человека) предпочитает поужинать в стейк-хаусе, но значительное число (20 человек) не любит стейки. Индийская и греческая кухня остались в меньшинстве, но собрали равное число голосов.

Однако абсолютно все отметили ресторан со шведским столом в качестве второго приоритета. Это выглядит хорошим компромиссом, и мудрый босс выбирает заведение со шведским столом для корпоратива. Можно ли построить аналогичный метод принятия решения на выборах?