Эдвард Шейнерман - Путеводитель для влюбленных в математику

Прибегнем к помощи компьютера. Программа, итерирующая f , даст такие результаты:

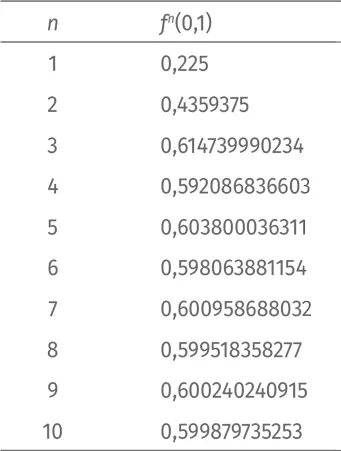
Заметим, что успешное итерирование все больше и больше приближает нас к 0,6. Есть хороший способ продемонстрировать это наглядно. Отметим на графике величины f (0,1), f ( f (0,1)), f ( f ( f (0,1))) и т. д. На оси абсцисс нанесем номера итераций, n . На каждом шаге будем отмечать значение f n( x ) («нулевая» итерация – это наше начальное число 0,1). Соединим все точки отрезками. Вот что получится:

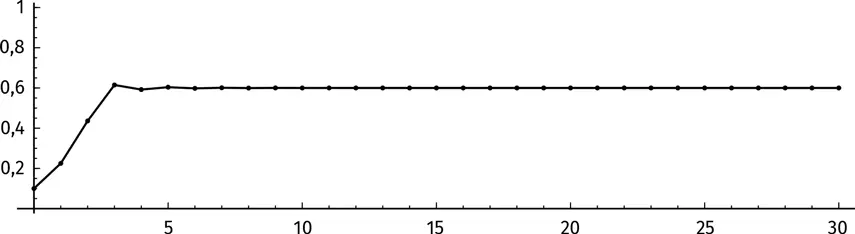
Мы видим, что итерации f ( x ) сходятся к числу 0,6.

А что, собственно, особенного в числе 0,6? Заметим, что

f (0,6) = 2,5 × 0,6 × (1–0,6) = 2,5 × 0,6 × 0,4 = 0,6.

Число 0,6 называют неподвижной точкой функции f , поскольку применение функции к этому числу не меняет его: f (0,6) = 0,6.

Продублируем эксперимент с другой функцией того же семейства; на сей раз возьмем множитель m = 2,8; таким образом, функция приобретает вид f ( x ) = 2,8 x (1 – x ). Как и в предыдущем случае, мы начнем итерирование с x = 0,1. Вот первые 10 значений:

Похоже, итерации выплясывают вокруг 0,64. Продолжим итерировать и построим график:

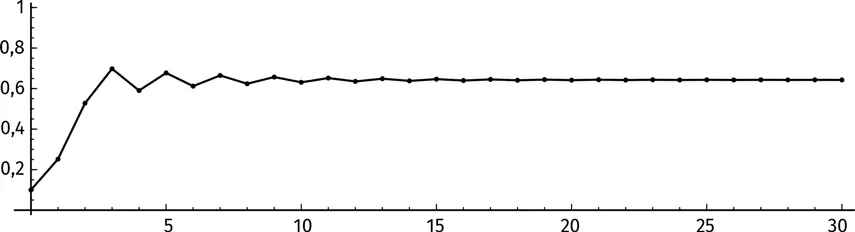
В пределах первых 10 итераций значения функции слегка колеблются вверх и вниз, но уже на 30-й они выравниваются. На какой величине? Это число между 0 и 1, такое, что f ( x ) = x . Нам остается решить незамысловатое уравнение:

Итерации f ( x ) = 2,8 x (1 – x ) сходятся к числу 0,642857.

Итерирование логистического отображения f ( x ) = m x (1 – x ) можно рассматривать в качестве простой эволюционирующей системы. Число x показывает состояние системы, а функция f диктует, как система эволюционирует при смещении на один шаг [210] Математики называют такие системы динамическими: нам дано начальное состояние и правило, по которому система меняется со временем. . В двух рассмотренных нами случаях ( m = 2,5 и m = 2,8) долгосрочное поведение системы приводит к «равновесию» в неподвижной точке функции.

Мы продолжим исследование итераций логистического отображения в случае m = 3,2. Как и в предыдущих случаях, мы начнем с х = 0,1. Вот первые десять значений:

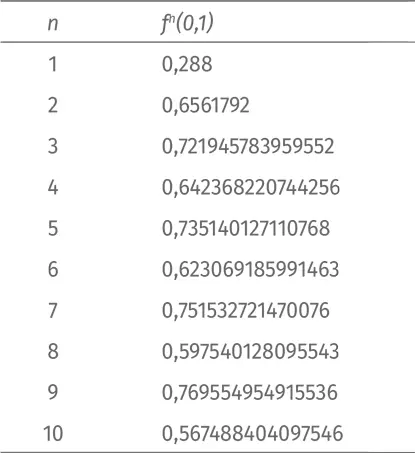
Что происходит? Итерации не сходятся к одной величине. Значения на четных шагах становятся меньше (это примерно 0,66; 0,64; 0,62; 0,6; 0,57), а на нечетных – растут (примерно 0,72; 0,74; 0,75; 0,77). Значения расходятся, а не сходятся!

Начертим график первых 30 итераций, чтобы изобразить наглядно проведение системы:

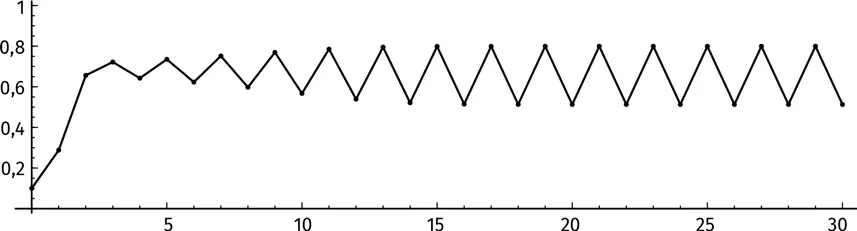
Посмотрите! Она не выравнивается к одному числу, а осциллирует [211] Колеблется, пульсирует (от лат. oscillari – качаться). – Прим. пер. между двумя величинами. Доведем вычисления до 50-й итерации. Вот последние строчки таблицы:

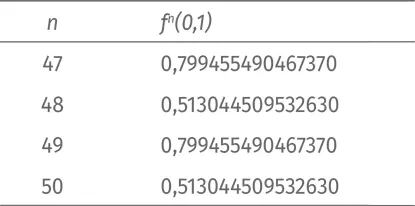
Долгосрочное поведение системы – осцилляция между двумя величинами, s = 0,799455… и t = 0,5130445… Эти числа таковы, что f ( s ) = t , а f ( t ) = s . Правило осцилляции можно изобразить так:

Какое еще поведение функции мы можем наблюдать, итерируя логистическое отображение? В следующем пункте нашей экспедиции m = 3,52. Посмотрим на график итераций f ( x ), f ²( x ), f ³( x ), …

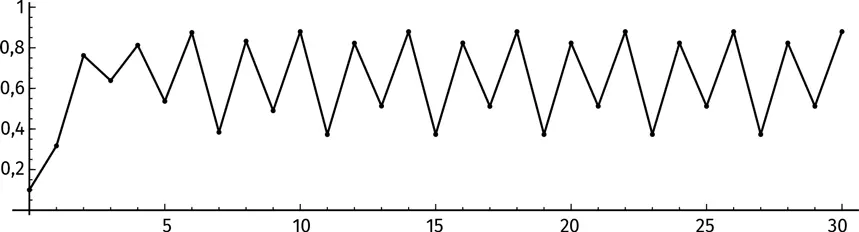
А вот таблица итераций:

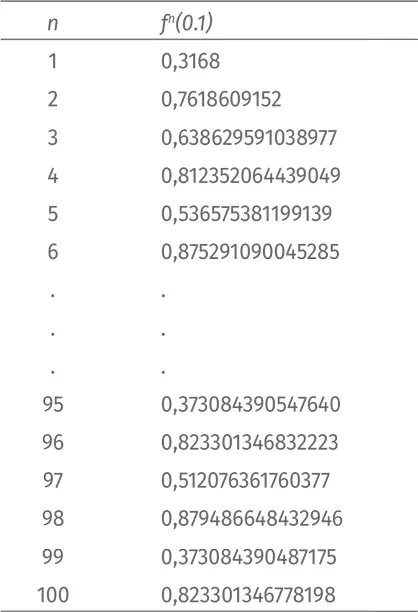
Долгосрочное поведение функции занятно, но по-прежнему стабильно. Система идет по циклу из четырех величин ad infinitum , как показано на иллюстрации.

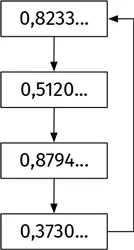
Мы проследили долгосрочное поведение итераций логистического отображения f ( x ) = m x (1 – x ). Итерации всегда приводили нас к стабильности. В некоторых случаях ( m = 2,5 и m = 2,8) система сходилась к одной величине: неподвижной точке функции f . В других случаях ( m = 3,2 и m = 3,52) она приобретала стабильный, предсказуемый ритм.

Жизнь хороша. Мы знаем исходную величину: x = 0,1. И мы знаем правило, по которому переходим от одного шага к другому: f ( x ) = m x (1 – x ). Разумеется, мы можем предвидеть поведение функции на любом шаге до бесконечности. Верно?

Настало время для последнего примера: m = 3,9. Доверим подсчет первых 10 итераций компьютеру:

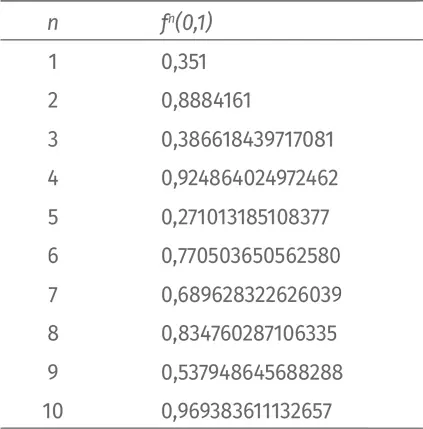
Что происходит? Неясно. Попробуем изобразить на графике первые 30 итераций:

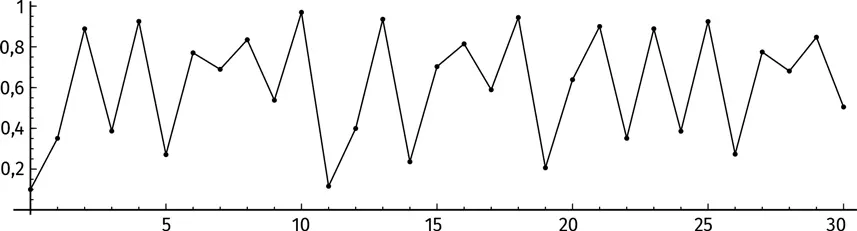
Хм… Ритм не прослеживается. Спокойствие, только спокойствие! Изобразим на графике первые 100 итераций.

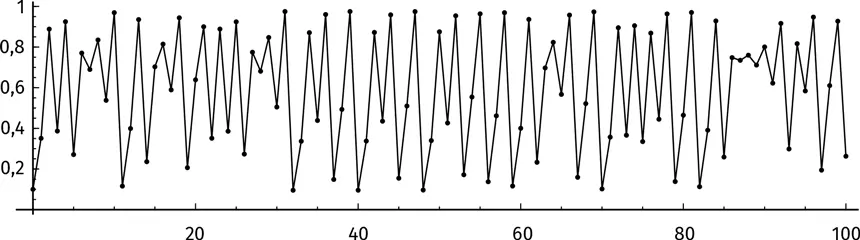
Колебания величин выглядят случайными. Разумеется, на самом деле это не так! Значение функции на каждом шаге можно точно подсчитать по формуле f ( x ) = 3,9 x (1 – x ). Но итерации логистического отображения никогда не приведут к стабильности. Хаос будет длиться вечно.

Великолепно: итерации беспорядочны, но система предсказуема на 100 %!

• Мы знаем исходную величину: x = 0,1.

• Мы знаем правило перехода от одного шага к другому: x → f ( x ) = 3,9 x (1 – x ).

Следовательно, мы можем вычислить состояние системы, скажем, на тысячной итерации. Верно?