Эдвард Шейнерман - Путеводитель для влюбленных в математику

Вообразим город с миллионом жителей. Один из тысячи болен. Другими словами, 1000 жителей больны и 999 000 здоровы.

Все жители проходят медицинское тестирование. Посмотрим, сколько будет положительных результатов, если тест эффективен на 98 %.

• Среди тысячи больных жителей положительный результат получит большинство, но не все. Их количество 1000 × 0,98 = 980.

• Среди 999 000 здоровых жителей большинство покинет поликлинику с радостной новостью об отсутствии болезни, но 2 % получат ложный результат. Это дает еще 999 000 × 0,02 = 19 980 положительных результатов.

В общей сложности 980 + 19 980 = 20 960 жителей получат положительный результат.

Теперь мы можем правильно ответить на поставленный вопрос: какова вероятность того, что вы больны, если ваш результат тестирования положительный?

Среди двадцати с лишним тысяч людей с положительным результатом всего лишь меньше тысячи действительно больны. Точная вероятность правильности теста в этом случае равна

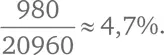
Вероятность того, что вам стоит беспокоиться, не равна 98 %! На самом деле вероятность того, что вы заражены этой редкой болезнью, меньше 5 %!

Стало быть, тесту грош цена? Не совсем.

Во-первых, если ваш лечащий врач имеет веские причины предполагать у вас наличие этого редкого заболевания, вы больше не «случайный» пациент. И если у вас действительно прослеживаются определенные симптомы, вероятность того, что вы заражены, уже не одна тысячная, а скажем, одна четвертая [204] Предположим, вы попали в категорию людей, где 25 % поражены болезнью. Какова вероятность того, что вы заражены, если результат тестирования положительный? Ответ – в конце главы. . В этом случае положительный результат тестирования имеет гораздо больший смысл, чем нестрого обоснованные выводы.

Во-вторых, если болезнь действительно опасна, тест, эффективный на 98 %, позволяет хорошо просеять большие массы населения на предмет наличия или отсутствия болезни. Пациенты с положительным результатом могут пройти вторую диагностику, дающую еще более точные результаты.

Разумеется, отрицательный результат – не повод успокаиваться полностью. Какова вероятность того, что он верен? (Ответ я дам в конце главы.)

Интуиция отказывается принимать тот факт, что тест, надежный на 98 %, может быть настолько несовершенным, но вычисления говорят сами за себя. Впрочем, голые цифры могут обманывать нашу интуицию. Попробуем нарисовать картинку.

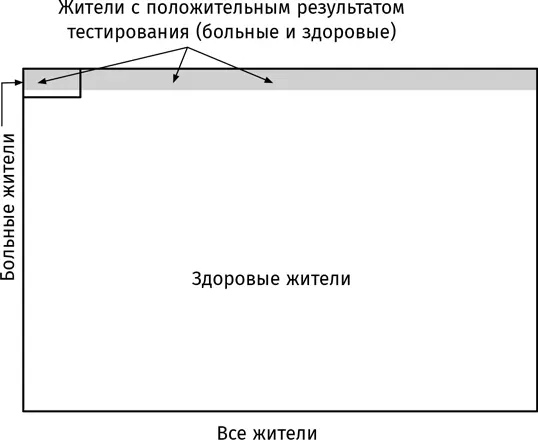
Заметим: диаграмма не соблюдает пропорции (0,1 % больных, эффективность теста 98 %).

На чертеже большой прямоугольник изображает все население. Фрагмент прямоугольника слева вверху обозначает группу больных жителей, оставшаяся часть – группу здоровых жителей. Серая полоса сверху – это все жители (из обеих групп) с положительным результатом. Белая область внизу – все жители (опять-таки из обеих групп) с отрицательным результатом

Чертеж иллюстрирует основные детали вышеописанной ситуации:

• болезнь редкая – крохотный фрагмент большого прямоугольника символизирует больную часть населения;

• тест верно диагностирует наличие болезни у подавляющей части больных – почти весь прямоугольник слева вверху закрашен серым;

• тест верно диагностирует отсутствие болезни у подавляющего большинства здоровых людей – огромная область большого прямоугольника остается белой;

• ключевой момент: большая часть серой полосы приходится на здоровых людей, поэтому вы, скорее всего, здоровы, если получили отрицательный результат, но не обязательно больны, если получили положительный.

Мы вычислили вероятность того, что пациент с положительными результатами медицинского тестирования действительно болен. Мы вообразили гипотетический город, где живет миллион человек, и посчитали численность разных категорий населения. Это был способ ad hoc [206] По особому случаю (лат.). – Прим. пер. . В общем случае мы должны руководствоваться языком теории вероятностей, и я завершу главу разъяснениями по этому поводу.

Для события A мы обозначаем P ( A ) вероятность того, что событие A произойдет, и 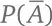– вероятность того, что событие A не произойдет; таким образом,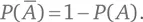

Для событий A и B мы обозначаем P (A ∧ B) вероятность того, что произойдут оба события – и A, и B .

Запись P (A|B) означает вероятность того, что из события A следует событие B ; это условная вероятность того, что A влечет за собой B . Формула Байеса [207] Томас Байес (1702–1761) – британский пресвитерианский священник, богослов и математик. – Прим. пер. говорит нам:

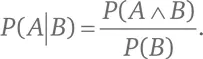
Надежность диагноза, вынесенного на основе упомянутого медицинского теста, может быть выражена на языке математики следующим образом. Пусть S означает, что некто заражен редкой болезнью, а T означает положительный результат тестирования. Таким образом:

• болезнь поразила 0,1 % населения, откуда следует, что P ( S ) = 0,001;

• тест дает верную информацию о наличии или отсутствии заболевания в 98 % случаев, откуда следует, что P ( T | S ) = 0,98;

• тест дает верную информацию о том, что человек здоров, в 98 % случаев, откуда следует, что 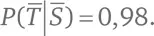Иначе говоря, тест ошибочен в 2 % случаев: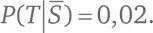

Вопрос: какова вероятность того, что пациент с положительным результатом тестирования действительно болен?

Если перевести задачу на язык символов, то мы ищем величину P ( S | T ). По формуле Байеса эта вероятность равна 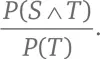Нам нужно узнать P (S ∧ T) и P ( T ).

Начнем хоть с P (S ∧ T) , хоть с P (T ∧ S) . По формуле Байеса

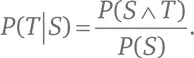
Мы знаем, что P ( T | S ) = 0,98, а P ( S ) = 0,001. Следовательно,