Эдвард Шейнерман - Путеводитель для влюбленных в математику

(A) Если подчеркнута цифра 3, пишем 7.

(B) Если подчеркнута не цифра 3, пишем 3.

Как это работает с нашим рядом?

Первая цифра 3. Выполняется условие (A). Мы получаем 0,7___.

Вторая цифра 8. Выполняется условие (B). Мы получаем 0,73___.

Третья цифра 7. Снова выполняется условие (B). Получаем 0,733___.

Четвертая цифра снова 3, по правилу (A) ставим семерку: 0,7337___.

Пятая цифра 6, по правилу (B) ставим тройку: 0,73373___.

Продолжая двигаться вдоль ряда подчеркнутых цифр, мы получим число x . В нашем примере число x = 0,73373…, а остальные цифры заполняются согласно условиям (A) и (B).

Вот процесс выстраивания x в пошаговом виде:

Число x зависит от нашей таблицы. Другая таблица даст другое x . Мы утверждаем, что в любой таблице x , выстроенное таким образом, не встречается в правой колонке; следовательно, взаимно однозначное соответствие между целыми положительными и действительными числами невозможно.

Начнем с самого верха. Очевидно, число x не идентично первому числу в правой колонке, и вот почему. Первая строка 1 ↔ Y 1. Если первая цифра Y 1после запятой – тройка, то первая цифра числа x после запятой – семерка; но если первая цифра Y 1после запятой – не тройка, то первая цифра числа x после запятой, напротив, – тройка. Ситуация выглядит так:

Таким образом, Y 1и x не совпадают. Какая бы цифра ни стояла после запятой в Y 1, первая после запятой цифра x другая. Следовательно, в первой строке таблицы x мы не найдем.

Двигаясь вниз по таблице, мы обнаружим, что во второй строке x тоже нет. Но если соответствие между ℤ +и ℝ взаимно однозначное, где-нибудь в правой колонке число x просто обязано возникнуть. Иными словами, x появляется в строчке k , где слева стоит целое положительное число k , то есть k ↔ Y k= x . Но мы все время будем сталкиваться с одной и той же проблемой. Какая цифра стоит в числе Y k на позиции k после запятой? Если тройка, то на соответствующей позиции в x обнаружится семерка; если не тройка, то на соответствующей позиции в x как раз тройка. Это выглядит так:

Эта проверка показывает, что x в правом столбце отсутствует. Мы, конечно, можем выстроить новую таблицу и поместить x на первую позицию. Но, если применить к новой таблице алгоритм с правилами (A) и (B), мы обнаружим, что в ней отсутствует некое число x '.

Вывод: всякая таблица будет ущербной! Таким образом, взаимно однозначное соответствие между ℤ +и ℝ построить невозможно.

Мы доказали, что мощности ℤ и ℤ +совпадают. И дело тут не только в том, что оба множества бесконечно велики, а еще в том, что мы построили биекцию.

ℤ +и ℝ тоже содержат бесконечное число элементов, но биекция между ними неосуществима. Так как любое целое положительное число – действительное, можно сказать, что ℝ «больше» ℤ +. Целых положительных чисел недостаточно, чтобы по одному сопоставить их со всеми действительными.

Мощность конечного множества – это число. Мощность множества A = {1, 3, 7, 9} равна четырем: | A | = 4. Но как зафиксировать мощность бесконечного множества? До выкладок Кантора математики довольствовались красивым символом ∞. Есть искушение написать: |ℤ +| = ∞ и |ℝ| = ∞, а затем сделать ошибочное заключение, что |ℤ +| = |ℝ|. Символ ∞ не передает всех особенностей, присущих мощностям бесконечных множеств.

Кантор решил исправить это и разработал новую систему чисел за пределами конечных. Такие числа называются трансфинитными и могут отразить мощность бесконечных множеств.

Мы выяснили, что ℤ + – «наименьшее» бесконечное множество. Что это означает? Предположим, X – бесконечное множество. Между X и ℤ +может быть биекция, а может и не быть. Но математики показали, что всегда есть взаимно однозначное соответствие между ℤ +и некоторой частью множества X : либо ℤ +и X равновелики, либо ℤ +равновелико с частью множества X . Грубо говоря, либо ℤ +и X имеют одинаковый размер, либо X больше.

Множества мощности ℤ +называют счетными . Это самые маленькие бесконечные множества. Кантор ввел символ 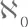для обозначения их мощности: 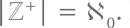Мощности ℤ и ℤ +совпадают, потому 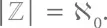Так как ℝ обширнее, чем ℤ +, логичным будет записать: 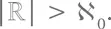Величина 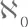обозначает мощность бесконечного множества, и это не обычное число. Его называют трансфинитным числом, причем 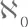– наименьшее из трансфинитных чисел [87] Символ א обозначает первую букву древнееврейского алфавита: алеф. Символ читают «алеф нуль». .

Мощности бесконечных множеств описывает целая вселенная трансфинитных чисел. Множества мощностью больше 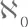называют несчетными , и математики показали, что есть новый «уровень бесконечности», на ступень выше 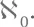Мы можем доказать, что существует множество X , которое обладает двумя свойствами:

1.

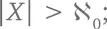
2. Нет множеств с мощностью между | X | и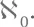

Таким множествам присвоили мощность 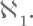Иначе говоря, 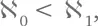и между этими двумя величинами нет других трансфинитных чисел.

Существует целая последовательность трансфинитных чисел. Она выглядит следующим образом: 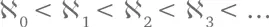и т. д. Иерархия подразумевает, что есть трансфинитное число, превышающее любое א k [88] Вообще говоря, из сказанного это не следует; существование таких чисел надо специально доказывать. – Прим. науч. ред. . Наименьшее трансфинитное число, превышающее любое א k , мы обозначаем א ω, и есть бесконечно много еще больших чисел!