Эдвард Шейнерман - Путеводитель для влюбленных в математику

Мы можем проиллюстрировать эту закономерность на графике. Будем отмечать число N по оси абсцисс и agap( N ) по оси ординат. Масштаб по оси ординат оставим обычным, а по оси абсцисс разница между делениями пусть постоянно возрастает в 10 раз (это называется логарифмическая шкала ):

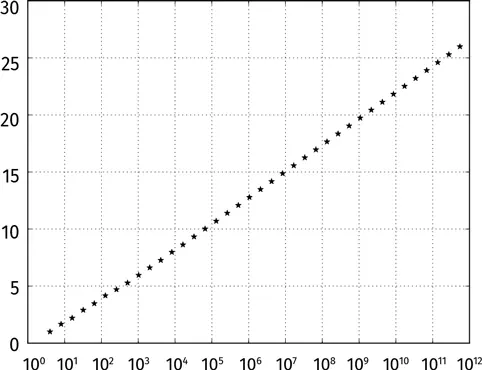
Обратите внимание: звездочки выстроились почти в прямую линию. Если присмотреться, левый нижний конец нашей кривой слегка загибается вверх.

Если бы звездочки на графике в точности выстроились в линию, мы получили бы следующую формулу, включающую число Эйлера:

N = e a + 1. (C)

Здесь а= agap( N ) Скажем, если N = 10 12, то agap( N ) ≈ 26,59. Для выполнения (C) необходимо, чтобы a ≈ 26,63, и наш результат близок к этому числу.

Три главы были посвящены трем важным числам: π, i, e . Хотите верьте, хотите нет, но все они встречаются в одной формуле (которую вывел Эйлер):

e i π + 1 = 0.

Формула поражает невероятным изяществом и простотой, однако как можно возводить число в мнимую степень?!

Мы знаем, как возвести e в целую положительную степень. Например, e³ = e × e × e . Отрицательная степень – это произведение дробей: 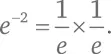Дробные степени могут быть выражены через квадратные корни, кубические корни и т. д.: 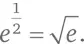Можно посчитать даже такую жутковатую величину, как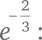

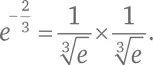
Но e iπне вписывается в эти стандарты. Нам нужен иной принцип [78] Я здесь пропускаю множество этапов вывода формулы Эйлера. Я хочу просто объяснить, что значит возводить число в мнимую степень, и дать общую картину доказательства. В полном виде оно включает тригонометрические выкладки и такие сложные вычисления, которым не место в этой книге. .

Мы знаем, что e представляет собой сумму бесконечного ряда:

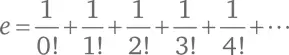
Для любого x значение e x будет:

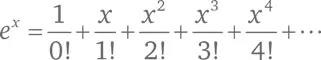
Скажем, в случае x = –1 мы получим знакомый по казусу со шляпами ряд (B):

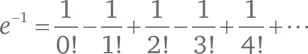
Чтобы узнать, чему равно e i π, подставим iπ вместо x :

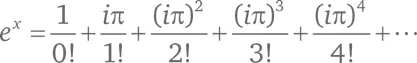
Чему равны числители дробей в этой сумме?

( i π) ² = ( i π) × ( i π) = i ² × π² = – π².

( i π) ³ = i × i × i × π³ = –1 × i × π³ = –i π³.

( i π) ⁴ = i ⁴ × π⁴ = π⁴.

( i π) ⁵ = – i π⁵.

( i π) ⁶ = –π⁶.

( i π) ⁷ = – i π⁷.

( i π) ⁸ = π⁸.

Элементы ряда поочередно оказываются то действительными, то мнимыми. Сгруппируем эти две категории элементов:

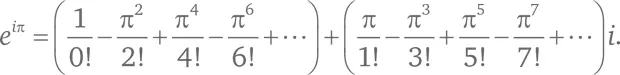
Оказывается, что выражение между первыми двумя скобками представляет собой в точности cos(π), то есть –1, а выражение между вторыми скобками равно sin(π), то есть 0. Таким образом,

e i π= cos(π) + i sin(π) = –1 + 0 i = –1.

Теперь мы понимаем, как возникла чудесная формула Эйлера.

«В бесконечность и дальше!» – таков был лозунг Базза Лайтера, бесстрашного космического рейнджера из мультфильма «История игрушек». Эта фраза вызывает смех, ибо абсурдна: куда уж дальше бесконечности? Если что-то бесконечно велико, то может ли существовать что-то большее? Такие вопросы кажутся безумными, и математики до поры до времени предпочитали их не задавать. Но в конце XIX века Георг Кантор [79] Георг Кантор (1845–1918) – немецкий математик, создатель теории множеств. Последние годы провел в психиатрической лечебнице. – Прим. пер. набрался смелости и стал искать ответ [80] Работы Кантора подвергались нещадной критике как со стороны математиков, так и со стороны философов и теологов. Но спустя некоторое время он добился признания как первооткрыватель новой области математики. . Интуиция подсказывает, что нет ничего больше бесконечности.

Оказывается, здесь интуиция нас подводит.

В математике все сложное объяснимо через простое. Если быть достаточно скрупулезным, то комплексные числа можно определить с помощью действительных, действительные – с помощью рациональных, рациональные – с помощью целых и т. д. Все здание математики покоится на фундаментальной концепции множества .

Множество – это просто набор объектов. Например, {1, 2, 5} – множество, состоящее из трех чисел [81] Обычно множество обозначают с помощью фигурных скобок. . Оно совпадает с множеством {1, 5, 2}, потому что порядок чисел в данном случае не важен. Кроме того, объект либо входит, либо не входит во множество. Входить во множество два раза нельзя. Множество {1, 1, 2, 5} совпадает с множеством {1, 2, 5}, второе появление числа 1 избыточно.

Если элемент входит в некоторое множество, математики используют значок ∈. Например, выражение 2∈ {1, 2, 5} следует понимать так: «Число 2 входит во множество, состоящие из чисел 1, 2, 5». Перечеркнутый значок показывает, что элемент не входит во множество; например: 3∉ {1, 2, 5}.

Число элементов, входящих во множество A , мы обозначаем | A |. Например, |{1, 2, 5}| = 3. Число | A | называют мощностью множества A .

Мощность такого рода множеств, как {1, 2, 5}, конечна. Однако мощность множества ℤ (все целые числа) бесконечна, как и мощность множества ℝ (все действительные числа).

Как сравнить размеры двух множеств? Простейший способ – пересчитать их элементы. Например, и у множества {1, 2, 5}, и у множества {3, 8, 11} мощность равна 3, стало быть, они равновелики.

Другой способ установить, что мощность множеств совпадает, – построить взаимно однозначное соответствие между их элементами [82] Математики называют взаимно однозначное соответствие биекцией. . Иными словами, нам не обязательно перебирать все элементы, достаточно ввести правило, по которому мы сопоставляем элемент из одного множества с каким-либо элементом из второго. Вот взаимно однозначное соответствие между множествами {1, 2, 5} и {3, 8, 11}: