Авинаш Диксит - Стратегические игры

Существует два типа путешественников. Тип «высокая стоимость» всегда называет сумму 100 долларов, а тип «низкая стоимость» — 50 долларов. Пусть h — доля в популяции игроков типа «высокая стоимость».

a) Составьте таблицу выигрышей для игры между двумя путешественниками, выбранными из популяции случайным образом.

b) Постройте график уровня приспособленности типа «высокая стоимость», отобразив значения h на горизонтальной оси. На том же рисунке разместите график уровня приспособленности типа «низкая стоимость».

c) Опишите все равновесия в этой игре. По каждому равновесию укажите, оно мономорфное или полиморфное и устойчиво ли оно.

S2.В разделе 5.Ашла речь о проверке на наличие эволюционно устойчивой стратегии в трижды повторяющейся дилемме заключенных в контексте игры в ценообразование в ресторанах.

a) Воспользовавшись рис. 12.10, дайте исчерпывающее объяснение того, почему популяция, состоящая только из игроков типа В, не может быть захвачена ни мутантами типа Н, ни мутантами типа О.

b) Объясните, почему популяция, состоящая только из игроков типа Н, может быть захвачена мутантами типа В и в какой степени ее могут захватить мутанты типа О. Соотнесите это объяснение с представленной в данной главе концепцией нейтральной устойчивости.

c) И наконец, объясните, почему популяция только из игроков типа О не может быть захвачена мутантами типа В, но может быть захвачена мутантами типа Н.

S3.Рассмотрите популяцию, в которой есть два фенотипа: один прирожденный коллективист (ни за что не сознается), второй прирожденный индивидуалист (охотно сознается). При случайном выборе членов этой популяции они получают те же выигрыши в однократной игре, что и выигрыши в представленной ниже дилемме заключенных из главы 4 в игре с участием мужа и жены. В повторяющемся взаимодействии популяции доступны две стратегии, такие же как в разделе 2: В (всегда сознаваться) и О (использовать стратегию «око за око», начав с отказа от признания вины).

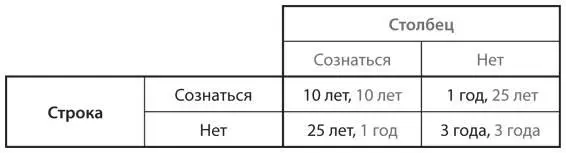
a) Предположим, пара игроков разыгрывает эту дилемму два раза подряд. Составьте для этой дважды повторяющейся дилеммы заключенных таблицу выигрышей.

b) Найдите все эволюционно устойчивые стратегии в этой игре.

c) Теперь прибавьте третью стратегию Н — «никогда не сознаваться». Составьте таблицу выигрышей для этой дважды повторяющейся дилеммы заключенных с тремя возможными стратегиями и найдите все эволюционно устойчивые стратегии новой версии этой игры.

S4.В игре в доверие («место встречи») в данной главе выигрыши отражали некую материальную ценность, получаемую игроками в случае различных исходов; например, это могли быть призы за успешно состоявшуюся встречу. Другие представители этой же популяции, наблюдая за ожидаемыми выигрышами (уровнем приспособленности) двух типов, могли определить, какой из них выше, и со временем имитировать стратегию, обеспечивающую более высокий уровень приспособленности. В итоге соотношение типов в популяции изменилось бы. Однако мы можем представить биологическую интерпретацию этой игры. Предположим, игроки столбца — всегда женского пола, а игроки строки — мужского. Когда два таких игрока встречаются, они вступают в брак, и их дети относятся к тому же типу, что и родители. Таким образом, эти типы могут размножаться или вымереть в зависимости от того, смогут они встретиться или нет. Формальная математика новой версии игры превращает ее в игру между двумя видами (хотя в биологии этого не происходит). Следовательно, доля игроков женского пола типа S (обозначим ее как x ) необязательно должна быть равной доле игроков мужского пола типа S (назовем ее y ).

a) Проанализируйте динамику изменения значений x и y с помощью методов, аналогичных использованным в данной главе в контексте игры «битва полов».

b) Найдите устойчивый исход или исходы этого динамического процесса.

S5.Вспомните о двух путешественниках из упражнения S1, которые должны назвать цену утерянных сувениров. Допустим, в популяции есть еще и третий фенотип путешественника. Он всегда смешивает стратегии, то есть использует смешанную стратегию, в одних случаях указывая стоимость сувенира 100 долларов, а в других 50 долларов.

a) На основании своих знаний о смешанных стратегиях в рациональных играх предложите смешанную стратегию, которую третий фенотип мог бы использовать в данной игре.

b) Составьте для этой игры таблицу выигрышей три на три, когда третий фенотип использует смешанную стратегию, предложенную вами пункте а.

c) Определите, будет ли смешивающий фенотип эволюционно устойчивой стратегией в данной игре. (Подсказка: проверьте, может ли тип «высокая стоимость» или тип «низкая стоимость» захватить популяцию смешивающего типа.)

S6.Рассмотрите упрощенную модель, в которой все получают электричество либо из солнечной энергии, либо из ископаемого топлива, когда в обоих вариантах присутствует неэластичное предложение [235]. (В случае солнечной энергии будем считать, что это неэластичное предложение необходимого оборудования.) Использование солнечной энергии требует больших первоначальных затрат, поэтому при низкой цене на ископаемое топливо (то есть когда его мало кто использует и существует высокий спрос на оборудование для использования солнечной энергии) они могут оказаться непомерно высокими. Напротив, когда многие используют ископаемое топливо, на него формируется высокий спрос (а значит, и цена), тогда как спрос на солнечную энергию (и ее цена) находится на относительно низком уровне. Предположим, таблица выигрышей двух типов потребителей энергии выглядит следующим образом:

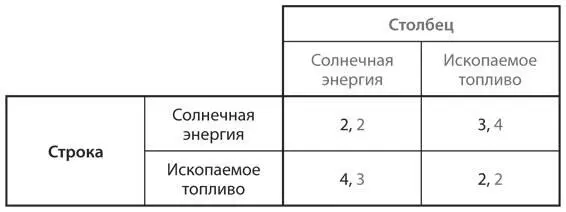
a) Опишите все возможные эволюционно устойчивые стратегии в этой игре относительно доли потребителей солнечной энергии s , а также объясните, почему каждый исход будет устойчивым или неустойчивым.

b) Допустим, в сфере производства оборудования для использования солнечной энергии существует значимая экономия от масштаба, благодаря чему экономия на затратах позволяет повысить выигрыши в ячейке таблицы («солнечная энергия», «солнечная энергия») до ( y, y ), где y > 2. Насколько большим должно быть значение y , чтобы в полиморфном равновесии s = 0,75?

S7.Существуют два типа участников забега (черепахи и зайцы), которые соревнуются друг с другом выбранными в случайном порядке парами. В этом мире зайцы неизменно побеждают черепах. Если в забеге участвуют два зайца, он заканчивается ничьей, но к концу забега оба зайца совершенно измучены. Когда в забеге участвуют две черепахи, соревнование также заканчивается ничьей, но в его ходе черепахи наслаждаются приятной беседой. Таблица выигрышей выглядит следующим образом (где с > 0):