Авинаш Диксит - Стратегические игры

c) Определите уровень приспособленности игрока, всегда выбирающего стратегию «око за око».

d) На основании ответов в пунктах b и c докажите, что при p > ( n — 2) / ( n — 1) тип, всегда отказывающийся от сотрудничества, имеет более высокий уровень приспособленности, а при p < ( n — 2) / ( n — 1) более высокий уровень приспособленности у типа, всегда выбирающего стратегию «око за око».

e) Если эволюция приводит к постепенному увеличению доли более приспособленного типа в популяции, каковы возможные равновесные исходы этого процесса для популяции, о которой идет речь в упражнении? (Другими словами, каковы возможные эволюционно устойчивые равновесия?) Проиллюстрируйте свой ответ с помощью графика уровней приспособленности.

f) В каком смысле большее количество повторений (более высокие значения n ) способствует эволюции сотрудничества?

U3.Предположим, в дважды повторяющейся дилемме заключенных из упражнения S3в популяции может существовать четвертый тип (тип С). Он не признает своей вины в первом раунде, но сознается во втором раунде каждого эпизода в двух подряд раундах игры против того же соперника.

a) Составьте таблицу уровней приспособленности четыре на четыре в этой игре.

b) Может ли новый тип С выступать в качестве эволюционно устойчивой стратегии данной игры?

c) В игре с тремя типами из упражнения S3типы В и О были эволюционно устойчивыми стратегиями, но тип О был нейтрально устойчивым, поскольку с ним могла сосуществовать небольшая доля мутантов Н. Докажите, что тип О не может быть эволюционно устойчивой стратегией в игре с четырьмя типами.

U4.Придерживаясь схемы, описанной в упражнении S4, проанализируйте эволюционную версию игры в розыгрыш очка в теннисе (см. рис. 4.14). Рассматривая подающих и принимающих игроков как отдельные виды, постройте рисунок, аналогичный рис. 12.15. Что вы можете сказать об эволюционно устойчивой стратегии и ее динамике?

U5.Вспомните о популяции животных из упражнения U1, борющихся за источник пищи, ценность которого составляет 200 калорий. Предположим, что в пункте b этого упражнения издержки в случае драки (для каждого игрока) равны 150 калорий. Представим также, что в этой популяции есть третий фенотип, который всегда смешивает стратегии, то есть использует смешанную стратегию, порой вступая в драку, а порой делясь пищей с другими.

a) На основании своих знаний о смешанных стратегиях в рациональных играх предложите разумную смешанную стратегию, которую третий фенотип мог бы использовать в данной игре.

b) Составьте таблицу выигрышей три на три для этой игры, когда третий фенотип использует смешанную стратегию, предложенную вами в пункте а.

c) Определите, будет ли смешивающий фенотип эволюционно устойчивой стратегией в данной игре. (Подсказка: проверьте, может ли тип, который всегда вступает в драку, или тип, который всегда делится пищей, захватить популяцию смешивающего типа.)

U6.Рассмотрим эволюционную версию игры между Бейкером и Катлером из упражнения U1в главе 10. В этот раз Бейкер и Катлер — не два человека, а два разных вида. Каждый раз при встрече они ведут следующую игру. Бейкер выбирает общий приз в размере 10 или 100 долларов. Катлер решает, как разделить приз, выбранный Бейкером; при этом Катлер может разделить приз либо в соотношении 50 на 50, либо в соотношении 90 на 10 в свою пользу. Катлер ходит первым, а Бейкер вторым.

В популяции есть два типа Катлеров: тип F выбирает справедливое разделение приза (50 на 50), тогда как тип G — корыстное разделение (90 на 10). Существует также два типа Бейкеров: тип S просто выбирает большой приз (100 долларов) независимо от действий Катлера, тогда как тип T выбирает большой приз (100 долларов), но при условии, что Катлер его разделит 50 на 50, и маленький приз (10 долларов), если Катлер выберет разделение 90 на 10.

Пусть f — доля типа F в популяции Катлеров, а значит, (1 — f ) — доля в этой популяции типа G . Пусть s — доля типа S в популяции Бейкеров, а значит, (1 — s ) — доля в этой популяции типа T .

a) Определите уровень приспособленности типов F и G относительно s .

b) Определите уровень приспособленности типов S и T относительно f .

c) При каком значении s у типов F и G одинаковый уровень приспособленности?

d) При каком значении f у типов S и T одинаковый уровень приспособленности?

e) На основании полученных выше ответов начертите график динамики популяций. Отобразите значения f на горизонтальной оси, а значения s — на вертикальной.

f) Опишите все равновесия в этой эволюционной игре, а также укажите эволюционно устойчивые равновесия.

U7.Вспомните упражнение S7. Как оказалось, зайцы весьма заносчивые победители. Каждый раз, когда они обгоняют черепах, они безжалостно высмеивают их медлительность. Бедные черепахи не только проигрывают забег, но и терпят оскорбления со стороны зайцев. Таблица выигрышей в этой игре выглядит так:

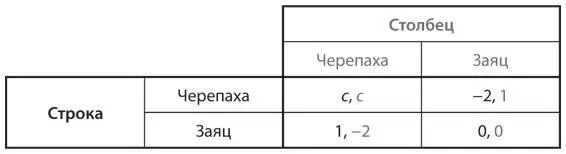
a) При каких значениях c уровень приспособленности черепах будет выше, чем у зайцев, если доля черепах t в популяции составляет 0,5? Чем этот результат отличается от ответа, полученного в пункте а упражнения S7?

b) При каких значениях c уровень приспособленности черепах будет выше, чем у зайцев, если t = 0,1? Чем этот результат отличается от ответа, полученного в пункте b упражнения S7?

c) Если c = 1, сможет ли один заяц захватить популяцию, состоящую только из черепах? Объясните, почему да или почему нет.

d) Насколько большим относительно t должно быть значение c в случае черепах, чтобы они были более приспособленными, чем зайцы?

e) Какой уровень t относительно c в полиморфном равновесии? При каких значениях c установится такое равновесие? Обоснуйте свой ответ.

f) Будет ли устойчивым полиморфное равновесие, найденное в пункте e? Почему да или почему нет?

U8 (рекомендуется использовать электронную таблицу).В данной задаче выполняется более глубокий анализ динамики популяции от поколения к поколению, о которой шла речь в упражнении S8. Поскольку математические расчеты могут быстро стать достаточно сложными и громоздкими, рекомендуем выполнить этот анализ с помощью электронной таблицы.

Опять же, рассмотрим популяцию с двумя типами X и Y со следующей таблицей выигрышей:

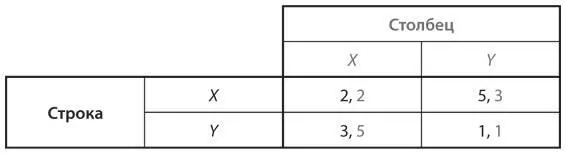
Вспомните, что динамику популяции от поколения к поколению определяет следующая формула: