Авинаш Диксит - Стратегические игры

a) Предположим, доля черепах t в популяции составляет 0,5. При каких значениях c уровень приспособленности черепах будет выше, чем у зайцев?

b) При каких значениях c уровень приспособленности черепах будет выше, чем у зайцев, если t = 0,1?

c) Если c = 1, сможет ли один заяц захватить популяцию, состоящую только из черепах? Объясните, почему да или почему нет.

d) Насколько большим относительно t должно быть значение c в случае черепах, чтобы черепахи были более приспособленными, чем зайцы?

e) Какой уровень t относительно c в полиморфном равновесии? При каких значениях c установится такое равновесие? Обоснуйте свой ответ.

S8.Рассмотрите популяцию с двумя типами X и Y со следующей таблицей выигрышей:

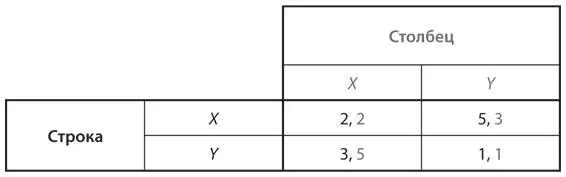
a) Определите уровень приспособленности X как функцию от x , где x — доля X в популяции, а также аналогично уровень приспособленности Y как функцию от y .

Предположим, динамика популяции от поколения к поколению подтверждает следующую модель:

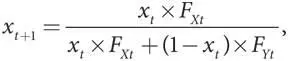
где x t — доля X в популяции за период t; x t+ 1 — доля X в популяции за период t + 1; F Xt — уровень приспособленности X за период t; F Yt — уровень приспособленности Y за период t .

b) Предположим, x 0, доля X в популяции за период 0, составляет 0,2. Чему равны F X 0и F Y 0?

c) Найдите значение x 1с помощью значений x 0, F X 0, F Y 0 в приведенной выше модели.

d) Чему равны значения F X 1и F Y 1?

e) Найдите значение x 2(округленное до пяти десятичных знаков).

f) Чему равны значения F X 2и F Y 2(округленные до пяти десятичных знаков)?

S9.Рассмотрите эволюционную игру между игроками зеленого и пурпурного типов со следующей таблицей выигрышей:

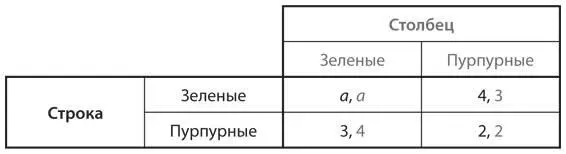
Пусть g — доля зеленых в популяции.

a) Определите уровень приспособленности пурпурного типа через g .

b) Определите уровень приспособленности зеленого типа через g и a .

c) Постройте график приспособленности пурпурного типа относительно доли g пурпурного типа в популяции. Покажите на нем же три линии, отображающие уровень приспособленности зеленых при a = 2, 3 и 4. Какой вывод на основании этого графика вы можете сделать о диапазоне значений а , обеспечивающих устойчивое полиморфное равновесие?

d) Допустим, значение а попадает в диапазон, найденный в пункте с. Чему равна доля зеленых g относительно a в случае устойчивого полиморфного равновесия?

S10.Докажите следующее утверждение: «Если стратегия строго доминирующая согласно таблице выигрышей в игре с участием рациональных игроков, то в эволюционной версии той же игры она исчезнет, каким бы ни был исходный состав популяции. Если стратегия слабо доминируемая, она сможет сосуществовать с некоторыми другими типами, но не в случае смешения всех типов».

U1.Рассмотрите игру в выживание, в которой представители большой популяции животных встречаются друг с другом и либо вступают в схватку, либо делят между собой источник пищи. В популяции есть два фенотипа: один всегда дерется, а другой всегда делится пищей. Будем исходить из того, что в популяции не могут появиться другие мутантные типы. Предположим, ценность источника пищи составляет 200 калорий и калорийность пищи определяет репродуктивную приспособленность каждого игрока. Если встречаются два типа, которые делятся пищей, каждый из них получает половину, но если игрок, который делится пищей, встречается с тем, кто всегда дерется, он сразу же уступает и задира получает всю пищу.

a) Допустим, издержки в случае драки (для каждого игрока) составляют 50 калорий, а когда встречаются два драчуна, каждый из них с равной вероятностью может либо победить в схватке и получить всю пищу, либо проиграть и вообще остаться без еды. Составьте таблицу выигрышей в игре с участием двух игроков, выбранных из популяции случайным образом. Найдите в этой популяции все эволюционно устойчивые стратегии. К какому типу можно отнести игру в данном случае?

b) Теперь предположим, что издержки в случае драки составляют 150 калорий. Составьте таблицу выигрышей и найдите все эволюционно устойчивые стратегии в популяции в этой ситуации. Какой тип игры будет в данном случае?

c) Воспользовавшись системой обозначений из игры «ястреб — голубь» раздела 6данной главы, укажите значения V и C в пунктах a и b и покажите, что ваши ответы в этих пунктах согласуются с анализом, представленным в данной главе.

U2.Допустим, в однократной игре «дилемма заключенных» следующая таблица выигрышей:

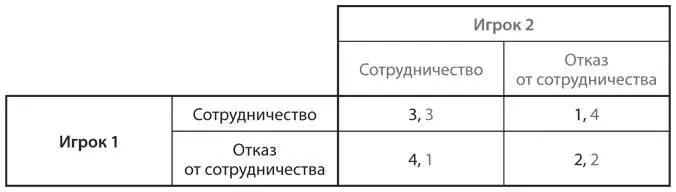
В большой популяции, в которой поведение каждого члена генетически предопределено, каждый игрок будет либо всегда отказываться от сотрудничества в любой игре «дилемма заключенных», либо использовать стратегию «око за око». (В дилемме заключенных, состоящей из нескольких раундов, этот игрок выбирает сотрудничество в первом раунде, а в каждом последующем делает то, что сделал соперник в предыдущем раунде игры.) Пары случайным образом выбранных из популяции игроков сыграют серии из n отдельных раундов этой дилеммы (при n ≥ 2). Выигрыш каждого игрока в одной полной серии (состоящей из n раундов игры) равен сумме выигрышей в n раундах.

Пусть p — доля игроков, всегда отказывающихся от сотрудничества, а (1 — p ) — доля игроков, всегда выбирающих стратегию «око за око». Каждый член популяции неоднократно играет в таких сериях дилемм, каждый раз против нового, выбранного случайным образом соперника. Игрок, использующий стратегию «око за око», всегда начинает новую серию с сотрудничества в первом раунде игры.

a) В таблице два на два покажите выигрыши игрока каждого типа в случае, если в ходе одной серии каждый игрок вступает в противостояние с соперником каждого из двух типов.

b) Определите уровень приспособленности (средний выигрыш в одной серии против случайно выбранного соперника) игрока, который всегда отказывается от сотрудничества.