Авинаш Диксит - Стратегические игры

На рис. 17.2дано геометрическое представление цели максимизации. Черные линии, обозначенные как c 1, c 2и c 3 — это изолинии, или линии уровня максимизируемой функции; на каждой такой кривой значение ( x — a ) h ( y — b ) k представляет собой постоянную величину и составляет c 1, c 2и c 3(где c 1 < c 2< c 3), как показано выше. Все пространство можно заполнить такими линиями, у каждой из которых свое значение постоянной, а у линий, расположенных в направлении «северо-востока», значения постоянных выше.

Очевидно, что самое высокое из возможных значение данной функции находится в точке касания Q линии эффективной границы и одной из изолиний [303]. Местоположение точки Q определяется тем свойством, что линия уровня, проходящая через Q , — касательная к линии эффективной границы. Точка касания — это общепринятый способ представления кооперативного решения Нэша в геометрическом виде [304].

В примере на рис. 17.1также можно вывести решение Нэша математически; для этого понадобится дифференциальное исчисление, но цели важнее способов их достижения (во всяком случае, в контексте изучения стратегических игр). Для того чтобы найти это решение, целесообразно записать X = x — a и Y = y — b . Таким образом, X — это величина излишка, получаемого игроком А, а Y — величина излишка игрока Б. Условие эффективности исхода гарантирует, что X + Y = x + y — a — b = v — a — b , что и представлет собой общую величину излишка, которую мы обозначим символом S . Тогда Y = S — X , а также

( x — a ) h ( y — b ) k = X h Y k = X h ( S — X ) k .

В решении Нэша X принимает значение, максимизирующее эту функцию. Элементарное исчисление говорит о том, что для определения значения X необходимо взять производную этого выражения по X и приравнять к нулю. Воспользовавшись правилами исчисления для поиска производных степеней X и произведения двух функций X , получим

hX h — 1( S — X ) k — X h k ( S — X ) k — 1 = 0.

Исключив общий множитель X h — 1( S — X ) k — 1, будем иметь

h ( S — X ) — kX = 0,

hY — kX = 0,

kX = hY

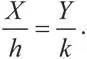
И наконец, выразив это уравнение через исходные переменные x и y , получим ( x — a )/ h = ( y — b )/ k , а это и есть формула Нэша. Вывод: три условия Нэша приводят к формуле, которую мы изначально обозначили как простой способ разделения излишка в процессе переговоров.

Эти три принципа, или заданные свойства, определяющие решение Нэша для кооперативных переговоров, — просты и даже привлекательны. Но при отсутствии эффективного способа убедиться, что стороны переговоров предпримут действия, предусмотренные в соглашении, они могут оказаться бесполезны. Игрок, которому выгоднее самостоятельно разрабатывать стратегию, чем использовать решение Нэша, может их просто проигнорировать. Если третейский судья может принудить выполнить решение, то игрок может отказаться от его услуг. Следовательно, кооперативное решение Нэша будет более убедительным при наличии альтернативной интерпретации в виде равновесия Нэша в некооперативной игре с двумя участниками переговоров. Это действительно осуществимо, и мы рассмотрим такой пример в разделе 5.

В данном разделе мы используем кооперативное решение Нэша в конкретной игре, а именно на втором этапе игры с последовательными ходами. В разделе 1мы исходили из предположения, что страховочные выигрыши игроков (BATNA) a и b имеют фиксированное значение. Но допустим, существует первый этап переговорной игры, на котором игроки могут выполнять стратегические ходы, направленные на манипулирование показателями BATNA в определенных пределах. После таких действий игроков на втором этапе игры появляется кооперативный исход Нэша. Игру данного типа называют переговорами с переменной угрозой. Какие манипуляции со значениями BATNA отвечают интересам ее участников?

На рис. 17.3 показаны возможные результаты манипулирования BATNA. Исходные значения страховочных выигрышей ( a и b ) — это координаты страховочной точки P в игре; решение Нэша в переговорной игре с такими страховочными выигрышами находится в точке Q . Если игрок А сможет увеличить значение BATNA так, чтобы переместить страховочную точку игры в позицию P 1, то решение Нэша, начинающееся в этой точке, приведет к исходу Q ´, что лучше для игрока А (но хуже для игрока Б). Следовательно, стратегический ход, улучшающий BATNA игрока, целесообразен. Например, если, идя на собеседование в другую компанию, вы уже имеете хорошее предложение о работе (более высокий показатель BATNA), то, по всей вероятности, получите от этого работодателя более выгодное предложение, чем при отсутствии первой альтернативы.

Рис. 17.3.Переговорная игра с манипулированием значениями BATNA

Вывод о том, что повышение BATNA может улучшить конечный результат, вполне очевиден, но следующий этап анализа менее понятен. Оказывается, если игрок А сможет сделать стратегический ход, который уменьшит BATNA игрока Б и переместит страховочную точку игры в точку P 2, то решение Нэша, начинающееся в этой точке, приведет к тому же исходу Q ´, который был получен, когда игрок А увеличил свой показатель BATNA настолько, что попал в страховочную точку P 1. Следовательно, этот альтернативный тип манипуляции также отвечает интересам игрока А. В качестве примера уменьшения BATNA соперника представьте ситуацию, в которой вы уже работаете в компании и хотите получить повышение. Ваши шансы возрастут, если вы станете незаменимым для работодателя, то есть если без вас у его бизнеса возникнут проблемы. В таком случае неблагоприятный исход ввиду отсутствия соглашения (когда работодатель не предложит повышения и вы уволитесь из компании) может повысить вероятность того, что работодатель пойдет вам навстречу.

И последний, еще более драматичный вариант развития событий: если игрок А сможет сделать стратегический ход, уменьшающий значения BATNA обоих игроков настолько, что страховочная точка игры переместится в точку P 3, это опять же приведет к тому же результату, что и вследствие предыдущих манипуляций. Этот ход равносилен угрозе, которая гласит: «Это навредит вам больше, чем мне».

В общем плане для игрока А важно переместить BATNA в данной игре в одну из точек, находящихся под линией PQ . Чем дальше на юго-восток передвинется точка BATNA, тем лучше для игрока А в свете конечного результата. Как всегда в случае применения угроз, задача не в получении низкого выигрыша, а в том, чтобы использовать его вероятность в качестве рычага для достижения более приемлемого исхода.