Авинаш Диксит - Стратегические игры

Конкуренция не всегда подразумевает использование цен в качестве стратегических переменных. Например, рыболовные флотилии могут конкурировать за более крупный улов. В таком случае имеет место конкуренция по количеству, а не по цене, рассмотренная в данном разделе. Мы опишем конкуренцию по количеству чуть ниже, а также в нескольких упражнениях, размещенных в конце главы.

Наш второй пример взят из политики. Он требует немного больше математических выкладок, чем мы обычно используем, но мы объясним интуитивные идеи, лежащие в их основе, с помощью слов и графиков.

Рассмотрим выборы с участием двух партий или двух кандидатов. Каждая сторона пытается отнять голоса избирателей у другой стороны посредством рекламы — либо позитивных рекламных объявлений, подчеркивающих достоинства самой партии или кандидата, либо негативной рекламы, сфокусированной на недостатках соперника. Для простоты будем исходить из предположения, что изначально избиратели не владеют никакой информацией и не отдают предпочтения ни одной из партий, поэтому формируют свое мнение исключительно под влиянием рекламы. (Многие сказали бы, что это точное описание американской политики, но более продвинутые исследования в области политологии подтверждают тот факт, что информированные, стратегически мыслящие избиратели все же существуют. Мы проанализируем их поведение более подробно в главе 15.) Для того чтобы упростить ситуацию еще больше, допустим, что доля избирателей, голосующих за партию, равна доле партии в общей сумме расходов на рекламу избирательной кампании. Назовем партии или кандидатов Л и П; если Л тратит на рекламу x миллионов долларов, а П — y миллионов долларов, то Л получит долю x / ( x + y ) голосов, а П — у / ( x + y ) голосов. Читатели, заинтересовавшиеся этой областью практического применения теории игр, найдут более общее описание соответствующих методов в специальной литературе по политологии.

Сбор средств на оплату такой рекламы требует определенных затрат; к их числу относятся деньги на рассылку писем и телефонные звонки; время и труд кандидатов, партийных лидеров и активистов; будущее политическое вознаграждение для лиц, сделавших крупные пожертвования, а также возможные политические издержки в случае, если такое вознаграждение станет достоянием гласности и повлечет за собой скандал. Для простоты анализа предположим, что все эти затраты пропорциональны прямым затратам на проведение кампании х и у . В частности, допустим, что выигрыш партии Л оценивается как процент голосов за вычетом расходов на рекламу: 100 x ( x + y ) — x . Аналогичным образом выигрыш партии П составляет: 100 у / ( x + y ) — у .

Теперь можем определить наилучшие ответы. Поскольку это нельзя сделать без вычислений, выведем математическую формулу, а затем объясним ее общий смысл на интуитивном уровне. Для заданной стратегии х партии Л партия П выбирает стратегию у , чтобы максимизировать свой выигрыш. Условие первого порядка можно найти, зафиксировав значение х и приравняв производную от 100 у / ( x + y ) — у по у к нулю. В итоге получим уравнение 100 x / ( x + y ) 2 — 1 = 0, или 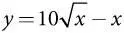. На рис. 5.2 показан график этой функции, а также аналогичный график функции наилучшего ответа партии Л, а именно .

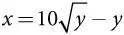Рис. 5.2.Наилучшие ответы и равновесие Нэша в игре «политическая реклама»

Посмотрите на кривую наилучших ответов партии П. По мере роста значения переменной x партии Л значение переменной у партии П сначала немного повышается, а затем снижается. Если другая партия размещает мало рекламных материалов, то реклама первой партии обеспечит высокую отдачу в виде голосов избирателей, поэтому на незначительное увеличение расходов другой партии на рекламу целесообразно ответить еще более существенным увеличением собственных расходов на рекламу в целях усиления конкуренции. Однако если другая партия уже вкладывает в рекламу солидные средства, то реклама первой партии обеспечит мизерную отдачу по отношению к затратам на нее, поэтому лучше ответить на повышение рекламных расходов другой партии сокращением собственных расходов.

Оказывается, кривые наилучших ответов двух партий пересекаются в точках максимума. Опять же, некоторые алгебраические манипуляции с уравнениями этих двух кривых позволяют получить точные величины равновесных значений x и y . Вы можете убедиться, что в данном случае значение каждой из переменных x и y равно 25, или 25 миллионов долларов. (Предполагается, что речь идет о выборах в Конгресс; выборы в Сенат и президентские выборы обходятся в наши дни гораздо дороже.)

Как и в игре в ценообразование, здесь мы имеем дело с дилеммой заключенных. Если обе партии сократят расходы на рекламу в равной пропорции, это никак не повлияет на долю голосов избирателей, но при этом обе партии сэкономят на расходах, а значит, получат более крупный выигрыш. В отличие от картеля производителей взаимозаменяемых продуктов (который поддерживает высокие цены и наносит ущерб потребителям), соглашение между политиками о сокращении объема рекламы, по всей вероятности, принесло бы пользу избирателям и обществу в целом, подобно тому как картель производителей взаимодополняющих продуктов привел бы к снижению цен и выгоде потребителей. Из решения данной дилеммы заключенных извлекли бы пользу все. В действительности Конгресс уже несколько лет пытается это сделать и даже ввел частичные ограничения, однако политическая конкуренция слишком ожесточенная для того, чтобы обеспечить полное или длительное разрешение этой дилеммы.

Но что если партии находятся в несимметричных ситуациях? Тогда может возникнуть асимметрия двух типов. Одна партия (скажем, П) может иметь возможность размещать рекламу по более низкой цене, поскольку у нее есть доступ к средствам массовой информации. Или рекламные расходы партии П могут быть эффективнее, чем у партии Л, — например, доля голосов Л может составлять x / ( x + 2 y ), тогда как доля голосов П — 2 y / ( x + 2 y ).

В первом случае партия П использует свой более дешевый доступ к рекламе, выбирая более высокий уровень расходов y для любого заданного значения x партии Л; иными словами, кривая наилучших ответов на рис. 5.2смещается вверх. Равновесие Нэша смещается вверх и направо вдоль неизменной кривой наилучших ответов партии Л. Таким образом, в итоге партия П потратит на рекламу больше, а партия Л меньше, чем раньше. Это сродни ситуации, когда побеждающая сторона как будто «играет мускулами», а проигрывающая как будто сдается перед таким натиском.